§3.4谐振子
§3.4.1 线谐振子的定态解
谐振子的势能为
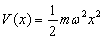（3.4.1）
势能随坐标变化的曲线绘在图3.4。
图3.4
任何一个物理体系必有势能为最小值的状态，否则体系是不稳定的，将向势能为负无限大的状态衰变下去。在势能极小值附近，可近似看作谐振子势。因此在众多物理问题中，谐振子近似是很重要的。谐振子问题有三种解法。海森堡利用其创立的矩阵力学先解决了谐振子的问题，后来，狄拉克利用算子代数的方法也给出了谐振子的解。第三种是下面的波动力学方法。
1、定态薛定谔方程
线谐振子满足的定态薛定谔方程为
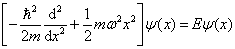（3.4.2）
线谐振子势是一个无限深的势阱，所以只有束缚态的解。引入无量纲参量
，
，
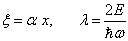（3.4.3）
方程（3.4.2）可以简化为
。
（3.4.4）
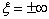为方程的正则奇点。
2、方程的解在
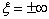处的渐近行为
当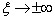 
时，方程（3.4.4）可以近似表示为
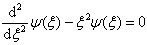（3.4.5）
显然， 
是上式的解。
但是，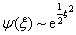 
不满足束缚态的要求，将其抛弃。若假设方程（3.4.4）的解为