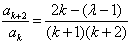(3.4.6)
(3.4.6)
将其代入(3.4.4)式,则可得到待定函数 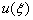 应满足的方程
应满足的方程
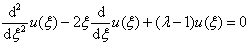 (3.4.7)
(3.4.7)
因为方程无奇点,所以在常点 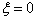 的邻域,
的邻域,  内,可将
内,可将 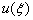 用
用 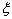 的幂级数来展开,即
的幂级数来展开,即
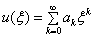 (3.4.8)
(3.4.8)
将上式代入方程(3.4.7),得
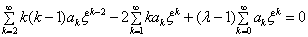 (3.4.9)
(3.4.9)
若令  ,代入上式第一项后,再将
,代入上式第一项后,再将  写成
写成 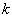 ,则上式可改写成
,则上式可改写成
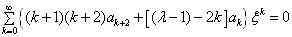 (3.4.10)
(3.4.10)
为使上式成立,必须要求其系数为零,即
 。
(3.4.11)
。
(3.4.11)
这是一个关于展开系数 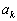 的递推公式。若已知
的递推公式。若已知 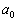 ,则可以依次求出所有偶数
,则可以依次求出所有偶数
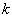 的
的
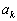 ,若已知
,若已知  ,则可以依次求出所有奇数
,则可以依次求出所有奇数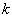 的
的
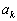 。于是,可以将
。于是,可以将
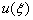 写成
写成
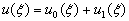 (3.4.12)
(3.4.12)
其中, 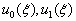 两个无穷级数分别为
两个无穷级数分别为
 (3.4.13)
(3.4.13)
对上述两个级数而言,相邻两项之比为