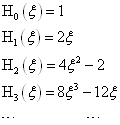 (3.4.21)
(3.4.21)
由 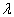 的定义和(3.4.3)式知能量本征值为
的定义和(3.4.3)式知能量本征值为
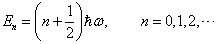 (3.4.22)
(3.4.22)
相应的本征波函数为
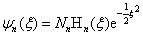 (3.4.23)
(3.4.23)
或者
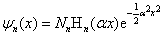 (3.4.24)
(3.4.24)
其中,归一化常数
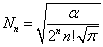 (3.4.25)
(3.4.25)
4、讨论
A、线谐振子的能级
(1)能量本征值 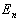 与分立的量子数
与分立的量子数 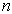 相关,能量是量子化的。
相关,能量是量子化的。
(2)最低的能量为 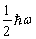 ,称为零点能。经典振子的零点能为零,玻尔-索末菲量子化条件的结果为
,称为零点能。经典振子的零点能为零,玻尔-索末菲量子化条件的结果为 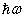 。
。
(3)能级是等间距的,间隔都是  。
。
(4)全部能级都是非简并的,这与定理三是一致的。
B、线谐振子的波函数
(1)若把波函数为零处的坐标值称为波函数的节点,则 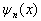 有
有
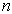 个节点。
个节点。
(2) 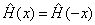 ,
由定理4可知,他必有确定的宇称。由厄米多项式的性质可知所以,由定理4可知,它必有确定的宇称。由厄米多项式的性质可知
,
由定理4可知,他必有确定的宇称。由厄米多项式的性质可知所以,由定理4可知,它必有确定的宇称。由厄米多项式的性质可知
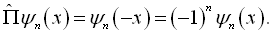 (3.4.26)
(3.4.26)