§3.6
一维定态问题的解题步骤
求解一维定态问题的基本步骤为：
1、由待求能量与位势的关系确定是否有束缚态的解
由问题给出的位势
的具体形式画出势能曲线图，明确要讨论的能量区域。若欲求的能量低于两个最外端位势的低者，则存在束缚态的解，否则，只有非束缚态的解。如果是非束缚态（势垒隧穿）问题，则将在下一章解决。
2、势能在全空间连续
可以利用波函数应满足的自然条件（单值、有限和连续）来求解。
例如，线谐振子问题。
3、势能分区均匀时的波函数
可以根据势能的性状，把求解区间分为几个区域，比较
与第
个区内位势
的大小，直接可以写出每个区域内波函数的形式。
当
时，有衰减解
(3.5.1)
其中，
(3.5.2)
当
时，有振荡解
(3.5.3)
其中，
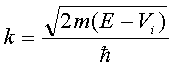(3.5.4)
4、势能分区均匀时波函数的边界条件
若势能存在间断点，因为在势能间断处，波函数的二阶导数不存在，在数学上并不要求一阶导数一定连续，而在物理上要求几率流密度连续。当间断点两边的势能皆为有限值时，要求波函数一阶导数连续是适当的，即。
；
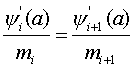(3.5.5)
在下面两种情况下，位势间断点两边的波函数一阶导数不连续：
（1）、
当间断点两边有一边为无穷大时，波函数一阶导数不连续，只能要求波函数连续，在§3.2.1中，无限深势阱即属于这种情况。
（2）、
对于
函数位势，
(3.5.6)
则要求波函数一阶导数满足
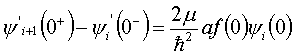(3.5.7)
5、求出能量本征值及归一化的本征波函数
确定能量的解析表达式或能量满足的超越方程，后者可用图解法或数值解法求出能量的数值。再利用波函数的归一化条件，确定波函数中剩下的最后一个常数，得到归一化的波函数。
6、特殊条件下的解
设已知一个哈密顿算符的解，即
(3.5.8)
如果
，或者
，则可以直接得到它们的本征解，式中，
与
皆为常数。
当势能平移
，即
时，
满足的本征方程为
(3.5.9)
显然，
与
的本征函数是一样的，而本征值变成
。
当坐标平移
，即
时，本征方程(3.5.8)变成
(3.5.10)
此时，
的本征值不变，而相应的本征函数的坐标变量由
变为
。