下面的定理适用于一维定态薛定谔方程
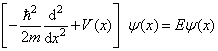 (3.1.6)
(3.1.6)
其中,位势满足 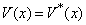 。
。
定理1
设 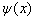 是上述方程的一个解,则它的复共轭
是上述方程的一个解,则它的复共轭 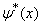 也是该方程的一个解,并且,与
也是该方程的一个解,并且,与 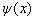 对应同一个能量本征值
对应同一个能量本征值 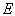 。
。
证明:将(3.1.6)式两端取复共轭,利用 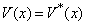 及
及 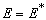 ,得
,得
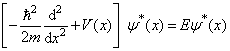 (3.1.7)
(3.1.7)
说明![]()
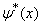 与
与
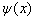 满足同一个方程,并且对应同一个能量本征值
满足同一个方程,并且对应同一个能量本征值
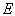 。
。
由此定理可知,若体系的某一个能量本征值
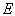 是非简并的,则它所对应的波函数一定是实函数,相应的概率流一定是零。
是非简并的,则它所对应的波函数一定是实函数,相应的概率流一定是零。
定理2
对于一维定态薛定谔方程,如果 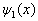 和
和  是对应同一个能量本征值
是对应同一个能量本征值
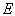 的两个独立的解,则有
的两个独立的解,则有
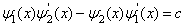 (3.1.8)
(3.1.8)
![]() 是任意常数。
是任意常数。
证明:
因为
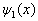 和
和
 皆满足(3.1.8)式,所以有
皆满足(3.1.8)式,所以有
 (3.1.9)
(3.1.9)
(3.1.10)
用
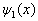 左乘(3.1.10)式,用
左乘(3.1.10)式,用
 左乘(3.1.9)式,再相减,得
左乘(3.1.9)式,再相减,得
 。
(3.1.11)
。
(3.1.11)
(3.1.11)可写为
 ,
(3.1.12)
,
(3.1.12)
积分就得到(3.1.8)
。
定理3
设势场  无奇点,如存在束缚定态,则其能级必是非简并的。
无奇点,如存在束缚定态,则其能级必是非简并的。
证明:
用反证法来证明此定理。假设
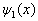 与
与
 是属于同一个能量本征值
是属于同一个能量本征值
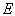 的两个独立的解,由定理2知,(3.1.8)式成立。根据束缚态的定义,当
的两个独立的解,由定理2知,(3.1.8)式成立。根据束缚态的定义,当  时,
时,
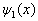 和
和
 均趋向于零,故(3.1.8)式中的常数
均趋向于零,故(3.1.8)式中的常数 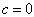 ,即,
,即,