。
在
及
区域，可除以
，得到
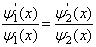(3.1.13)
积分后，有
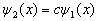(3.1.14)
即 
与 
相关，原来的假设不成立。
若 
无奇点，那末，
在
或
的零点也都连续，在零点两侧区域中得出的常数
将相同，这时定理必成立。如果
有奇点，在这点
而
不连续时，此定理可能不成立。
由此定理，再考虑到定理1，容易看出以下推论成立。
推论
一维束缚定态一定是实函数（整体复常数系数除外）。
定理4
设一维势能无奇点，具有空间反演不变性，则其束缚定态都有确定的宇称。
证明： 对一维定态薛定谔方程作反演，并考虑到
，
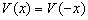有
。
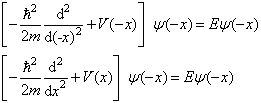(3.1.15)
可见
与
都是属于同一个能量本征值 
的束缚定态解。由定理3可知这两个解是不独立的，即
。
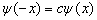(3.1.16)
再作一次反演，得到
，
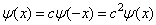(3.1.17)
于是，有
。
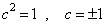(3.1.18)
当 
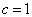时，
称之为偶宇称态；
当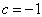 
时，
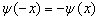
称之为奇宇称态。