§箱归一化
假设粒子在
的范围内运动，则它的波函数是可以归一化的，当
的值很大时，可作为粒子在无穷大的范围内运动的一个近似。对于三维问题而言，相当于粒子被限制在一个边长为2
的正方形箱子中运动，这时的波函数也是可以归一化的，此即自由粒子波函数的箱归一化。
在上述限制下，粒子是不可能处于箱外的，故在箱外的波函数为零。在箱内，设粒子动量或者动能算符的本征函数仍为
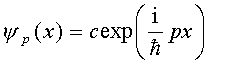(3.1.17)
作自由运动的粒子出现在箱的两端（
和
）处的概率幅应该是相同的，即
(3.1.18)
此即所谓周期性条件。将(3.1.17)式代入(3.1.18)式，有
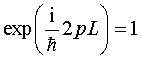(3.1.19)
由
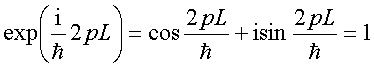(3.1.20)
可知
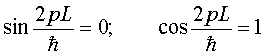(3.1.21)
进而得到
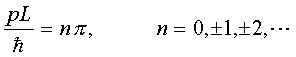(3.1.22)
于是动量
的取值是断续（分立）的，0即
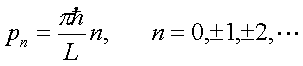(3.1.23)
能量本征值也是断续的，即
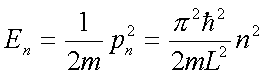(3.1.24)
通常把力学量（动量、能量等）本征值取断续（分立）值称之为取值量子化。由上式可知，随着箱的尺度
的增大，能级的间距变小，当
时，能级的间距趋向于零，或者说能级变成连续的，这正与自由粒子能量本征值是连续的相吻合。
利用归一化条件
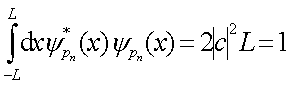(3.1.25)