其次，讨论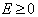 
的情况。
当 
时，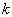 
为正的实数，(3.2.2)和(3.2.3)式即为其两个特解。若 
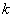的取值范围选为从负无穷到正无穷,
则上面两式可以统一写成
(3.2.9)
式中，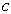 
是归一化常数，
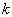为任意实数，可连续取值， 
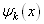是动量 
及能量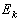 
的共同本征函数，
。
(3.2.10)
当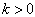 
时，表示粒子向右运动，当 
时，表示粒子向左运动。能量最低的状态，称为基态。自由粒子的基态就是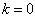 
的态。高于基态能量的状态称为激发态。自由粒子的激发态就是 
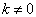的态。对于激发态来说,
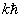与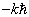 
对应同一个能量本征值，或者说，同一个能量本征值对应两个不同的本征波函数，称能量本征值简并度为2。
(3.2.2)及(3.2.3)式给出的波函数不是平方可积的波函数，无法使用归一化条件。由前所述，这时要归为
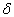函数，由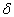 
函数的定义及德布罗意
关系可将(3.2.2)及(3.2.3)写为
。
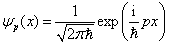(3.2.11)
由以上可见，对于自由粒子，量子力学所得到的动量谱和能量谱与经典力学是一样的。