§3.2.2
无限深方势阱
通常把势能分区均匀的位势称为方形位势，或者梯形位势。一维无限深方势阱是方形势阱中最简单的一种特殊情况，它是量子力学中少数几个可以得到解析解的问题之一。
1、能量本征方程
一个质量为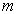 
的粒子处于如图3.1所示的一维无限深方势阱中，
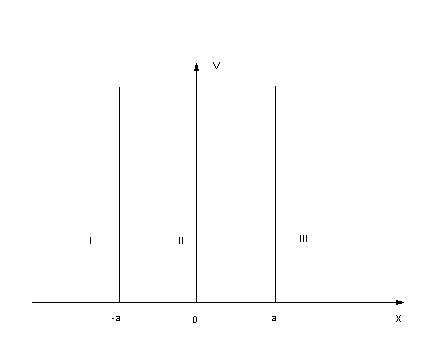
图
3.1
其势能的表达式为
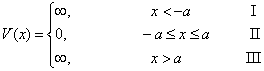（3.2.12）
由于势能是分区均匀的，故可以沿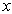 
轴将其分为三个区域，分别用Ⅰ、Ⅱ和Ⅲ来标志它们，三个区域中的势能分别是 
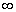、0和 
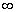。于是，可以在三个不同的区域中分别写出相应的定态薛定谔方程
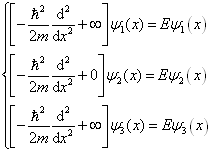（3.2.13）
式中，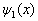
、 
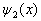和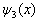 
分别表示在区域Ⅰ、Ⅱ和Ⅲ中的波函数。在Ⅰ和Ⅲ区中，势能皆为无穷大。如果粒子在Ⅰ和Ⅲ区中波函数不为零，则其在Ⅰ和Ⅲ区的概率就不为零，由于在Ⅰ和Ⅲ区中的势能皆为无穷大，因此体系的平均能量就是无穷大。这显然最不稳定的，也是不可能的。因此在Ⅰ和Ⅲ区中波函数必为零。这样，在三个不同的区域中，方程的解分别为
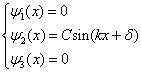（3.2.14）
其中，
。
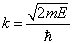（3.2.15）
2、能量本征值和本征函数
由于空间波函数是实波函数，所以概率流必处处为零，即，概率流连续的要求自动得到满足。因此处理此类问题时，不必考虑波函数微商的连续性。仅考虑波函数的连续性即可。在 
处，波函数应分别满足
（3.2.16）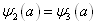
（3.2.17）