将（3.2.14）式分别代入（3.2.16）与（3.2.17）式，得
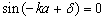（3.2.18）
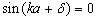（3.2.19）
由（3.2.18）与（3.2.19）式知
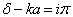（3.2.20）
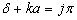（3.2.21）
其中，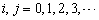 
。用（3.2.21）减去（3.2.20）式，有
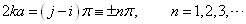（3.2.22）
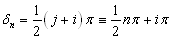（3.2.23）
在上式中，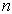 
的取值本应该从0开始，但若 
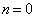，则 
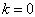，进而使得三个区域的波函数皆为零，这意味着粒子不存在，故弃之。
将（3.2.22）式代入（3.2.15）式，得能量本征值
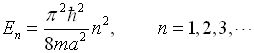（3.2.24）
能量本征值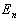 
与整数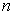 
有关，将整数 
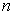称之为量子数。 
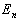也称之为粒子的能级。由此可知，无限深势阱中粒子的能量本征值是量子化的。这里量取值量子化是边界条件约束的结果。
将（3.2.22）和（3.2.23）代入（3.2.14）式，得能量本征函数
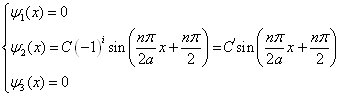（3.2.26）
再利用波函数的归一化条件
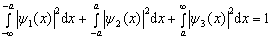（3.2.27）
来求出归一化常数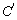 
，不管 
是奇数还是偶数，都有