这就是连带勒让德（Legendre）方程。在
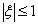区域内，上述方程有两个正则奇点 
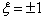，其余各点均为常点。数学上已经证明（附录），仅当
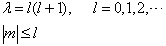(4.4.20)
时，方程(4.4.19)才有满足波函数物理要求的解，即连带勒让德多项式解
(4.4.22)
利用连带勒让德多项式的正交归一关系
(4.4.23)
可以得到归一化的波函数
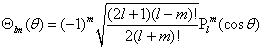(4.4.24)
满足
(4.4.25)
最后，算符
的本征值和本征函数为
(4.4.26)
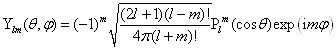(4.4.27)
其中，
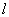称为轨道角动量量子数，
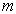称为磁量子数，
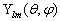是球谐函数。球谐函数满足的归一化条件为
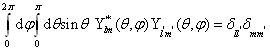(4.4.28)
为了使用方便，下面列出前几个球谐函数：
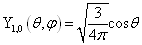
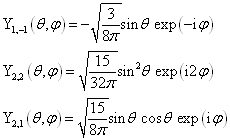
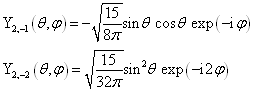(4.4.29)
整理以上结果得到
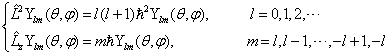(4.4.30)
总结：
1．由以上推导过程可以看出，由于对状态波函数提出的物理要求，即所谓波函数标准条件，才导致了算符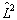 
与
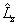的本征值的量子化的。
2．除了
的基态外，算符
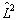的所有本征值都是简并的，且简并度为 
。
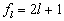3．
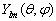是算符
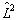与
的共同本征态，这两个力学量可以同时取确定值。而且由下面的讨论可知，本征函数系
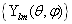是算符
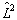与
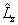的共同完备本征函数系。