§4.
5. 1 完备本征函数系
首先以一维动量本征函数为例说明完备本征函数这一概念。一维动量本征函数显然有以下性质：
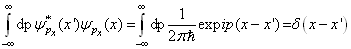(4.5.1)
(4.5.1)称为一维动量本征函数的封闭性。任何一个定义于
上的函数
都能够向这一函数系展开。
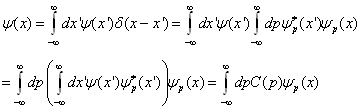(4.5.2)
式中
。
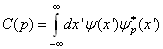如前所述，
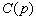的物理意义是动量
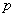出现的概率幅，这样
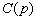也可以看作波函数，是动量表象的波函数。
定义在
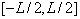上的箱归一化动量本征函数也有这样性质。只是积分要变为求和。
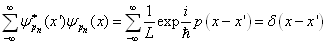(4.5.3)
定义在
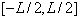上的任意一个函数
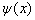都可以用函数集
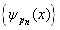展开，
(4.5.4)
式中
。
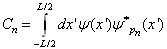如果把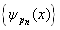 
看作无穷维希尔伯特空间的基，
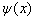看作这一空间的一个矢量，则(4.5.1)表示无穷（可数）维希尔伯特空间的任一个矢量向基的展开。在量子力学中，叠加原理成立。基的任意叠加仍表示体系的一个状态。这样，
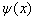可称为态矢量，
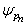称为本征矢量。零矢量及所有的态矢量
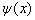构成了一个量子体系的无穷维希尔伯特空间，
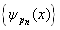构成了这一空间的完备基，
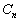是态矢量 
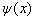的分量。
定义于
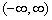上的
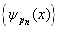是否也可看作为无穷（不可数）维希尔伯特空间的基呢？按数学上的严格定义，希尔伯特空间所有矢量的模都必须是有限的，而
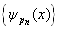的模都是无穷大，这样
就不是希尔伯特空间的矢量。但物理上具有连续本征值的算符是必不可少的，相应的不能归一或归为
函数的本征函数也就必不可少。为这一物理要求，就要扩大原来严格定义的希尔伯特空间，把那些模为无穷大，但与其它态矢量的内积（例如上述
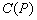）是有限的态矢量也包含进来。这样的空间称为物理的或扩大的希尔伯特空间。
在最一般情况下，一个算符
可能既有分立谱，又有连续谱。设
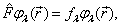
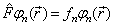(4.5.5)
则完备本征函数系可定义为，若在每个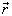 
处，态空间任一态矢量
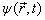总可以展开为
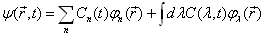(4.5.6)
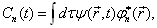
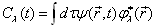(4.5.7)
即，在每个 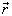处，右边的无穷级数都收敛到左边的
，则称
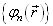是完备的函数系。例如，上述
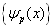是完备的。