推广上述结论到一个任意的线性厄米算符就有，任一个线性厄米算符的全部线性无关的本征矢量
构成了相应的希尔伯特空间的基矢，而且
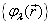是完备本征基矢（函数系）。
在分立本征值谱情况下，可证明这一结论。对于一般情况，严格证明这一结论，并非容易，但物理学总是假定它成立。
将(4.5.7)代入(4.5.6)得
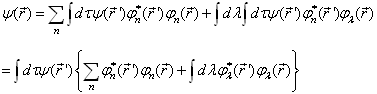(4.5.8)
因为
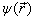是任意的，所以
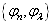应满足本征矢的封闭性
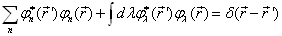(4.5.9)
如果
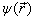归一的，则
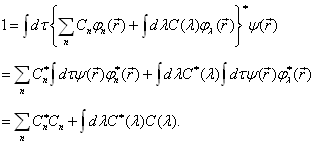(4.5.10)
在有简并时，算符同一个本征值的本征矢可能不正交，但我们总可以用施密特方法使其变成正交的。以后我们总假定线性无关的本征矢是正交归一（或归一为
函数）的。这时，上述结论也成立。只是求和时也要简并态指标进行。
§4,
5. 2 共通完备本征函数系
当有简并时，就意味着仅一个算符的本征值不能将态完全确定下来，必须引入另外的算符才能将态完全确定下来。这时，这个态就是两个算符共同本征态。
实际上，并不是任意两个算符都可以有完备的共同本征函数系的，当且仅当两个算符相互对易时，它们才可能存在完备的共同本征函数系，或者说，它们才可能同时取确定值。下面让我们来证明它。
定理1
若算符
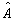与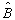 
有共同的完备本征函数系
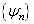，即
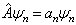(4.5.11)
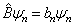(4.5.12)
而且
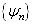是完备的，则必有
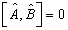(4.5.13)
证明：对于算符
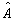和
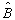的共同本征函数系 
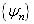，利用(4.5.11)和(4.5.12)式，有
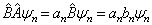(4.5.14)
(4.5.15)
于是，
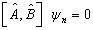(4.5.16)
对于任意态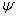 
，它总可以向完备系
作展开
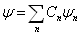(4.5.17)
用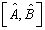 
从左作用上式两端，得
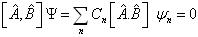(4.5.18)
根据
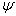的任意性知，
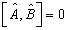(4.5.19)