定理2
若算符
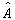 与
与
 满足对易关系
满足对易关系
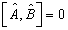 ,且算符
,且算符
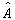 满足本征方程(4.5.11)的解是无简并的,则
满足本征方程(4.5.11)的解是无简并的,则
 也必是算符
也必是算符
 的本征态。
的本征态。
证明:用算符
 作用(4.5.11)式两端,有
作用(4.5.11)式两端,有
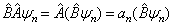 (4.5.20)
(4.5.20)
由上式可知
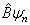 也是算符
也是算符
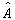 的对应本征值
的对应本征值
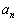 的本征态,因为
的本征态,因为
 的本征态是无简并的,它与
的本征态是无简并的,它与
 只能相差一个常数因子
只能相差一个常数因子 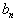 ,即
,即
 (4.5.21)
(4.5.21)
说明
 不但是算符
不但是算符
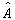 的本征态,而且也是算符
的本征态,而且也是算符
 的本征态。
的本征态。
当算符
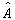 的本征值有简并时,可以证明上述结论也是正确的,但是,此时的共同本征函数系需要加以适当选择(参阅喀兴林,高等量子力学,高教出版社,1999年,第47-49页)。
的本征值有简并时,可以证明上述结论也是正确的,但是,此时的共同本征函数系需要加以适当选择(参阅喀兴林,高等量子力学,高教出版社,1999年,第47-49页)。
例如,
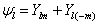 与
与 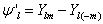 都是
都是  的本征函数,而不是
的本征函数,而不是
 的本征函数,但如果适当重新组合,则会得到
的本征函数,但如果适当重新组合,则会得到  与
与  的共同本征函数,
的共同本征函数,
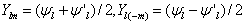 。
。
一般说来,若算符
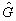 的本征值
的本征值 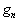 是
是
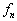 度简并的,即
度简并的,即
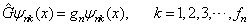 (4.5.22)
(4.5.22)
对于本征值
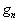 存在
存在
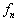 个线性独立的简并波函数,总可以将其选为正交归一和完备的。
这时任一波函数展开式为,
个线性独立的简并波函数,总可以将其选为正交归一和完备的。
这时任一波函数展开式为,
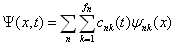 (4.5.23)
(4.5.23)
其中,展开系数
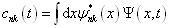 (4.5.24)
(4.5.24)
那么,
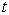 时刻在
时刻在
 态上测得
态上测得
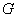 取
取
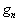 值的几率为
值的几率为
 (4.5.25)
(4.5.25)
这里本征值谱是分立谱,如连续,则求和化为积分。
§4. 5. 3力学量完全集
由上述两个定理可知,若算符的本征值是简并的,仅由其本征值无法惟一地确定其本征态。若要惟一地确定其本征态,必须再加上另一些与之对易的算符的本征值才可。例如,仅由
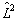 的本征值不能确定体系状态,必再加上
的本征值不能确定体系状态,必再加上
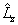 的本征值才能确定体系状态。这样,为了完全确定一个体系的状态,我们定义力学量完全集。
的本征值才能确定体系状态。这样,为了完全确定一个体系的状态,我们定义力学量完全集。
定义:如果有一组彼此独立而且相互对易的厄米算符
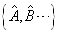 ,它们只有一组共同完备本征函数集,记为
,它们只有一组共同完备本征函数集,记为 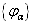 ,
,  可以表示一组量子数,给定一组量子数后,就完全确定了体系的一个可能状态,则称
可以表示一组量子数,给定一组量子数后,就完全确定了体系的一个可能状态,则称
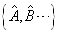 为体系的一组力学量完全集。
为体系的一组力学量完全集。
这里所谓的彼此独立算符是指,
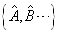 中的任一个算符都不是其它算符的函数,例如
中的任一个算符都不是其它算符的函数,例如  是彼此独立的,而
是彼此独立的,而 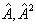 就不是;‘只有一组’意味着如果减少其中任一个算符,余下那些算符的共同完备本征函数集就有任意性,这也就是说,
就不是;‘只有一组’意味着如果减少其中任一个算符,余下那些算符的共同完备本征函数集就有任意性,这也就是说,
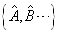 是完全确定体系状态所需要的最少数量的一组算符。例如,一维谐振子的宇称算符和体系的哈密顿算符
是完全确定体系状态所需要的最少数量的一组算符。例如,一维谐振子的宇称算符和体系的哈密顿算符
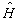 是对易的,但完全确定体系状态却只要
是对易的,但完全确定体系状态却只要
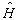 就可以了。完全确定体系的一个可能状态所用的算符组可以不同,所用算符的个数大于或等于体系自由度的数目。例如,一维自由粒子的态函数,可以用动能及运动的方向
就可以了。完全确定体系的一个可能状态所用的算符组可以不同,所用算符的个数大于或等于体系自由度的数目。例如,一维自由粒子的态函数,可以用动能及运动的方向 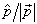 这两个独立而相互对易的物理量确定其状态。
当然,对于确定体系的态函数说来,这两个力学量和起来的作用等价于一个力学量的作用,即动量的作用,这两组力学量确定的都是动量本征态。一维自由粒子的态函数也可以用宇称及动能来确定。
这两个独立而相互对易的物理量确定其状态。
当然,对于确定体系的态函数说来,这两个力学量和起来的作用等价于一个力学量的作用,即动量的作用,这两组力学量确定的都是动量本征态。一维自由粒子的态函数也可以用宇称及动能来确定。
以上讨论说明,确定一个体系态函数的力学量完全集所包含的力学量,可以是不同的力学量,或不同数目的力学量。但必然存在这样一组力学量完全集,它所包含的力学量的数目等于体系自由度的数目组。例如,对于三维粒子,动量三个分量或者坐标三个分量都构成其力学量完全集,数目都是3。
因为
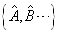 中的任一个算符的本征函数都构成完备本征函数系,而其余算符都与它对易,所以
中的任一个算符的本征函数都构成完备本征函数系,而其余算符都与它对易,所以
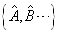 必有共同完备本征函数集。如果一组算符不能都相互对易,由前述定理可知,则即使它们有共同本征函数,这些共同本征函数也不能构成完备本征函数集。一般地证明本征函数集的完备性是个复杂的问题。但如果体系的一组力学量完全集中包含有体系的哈密顿算符
必有共同完备本征函数集。如果一组算符不能都相互对易,由前述定理可知,则即使它们有共同本征函数,这些共同本征函数也不能构成完备本征函数集。一般地证明本征函数集的完备性是个复杂的问题。但如果体系的一组力学量完全集中包含有体系的哈密顿算符
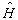 ,而
,而
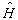 的本征值有下确界,无上界,则这组力学量完全集的共同本征函数集是完备的(曾谨言,量子力学,卷1,第二版,科学出版社,1997,第199-203页)。
的本征值有下确界,无上界,则这组力学量完全集的共同本征函数集是完备的(曾谨言,量子力学,卷1,第二版,科学出版社,1997,第199-203页)。