§4.
6 平均值和不确定关系
如前所述,当且仅当两个算符相互对易时,才存在共同完备本征函数系,这就意味着它们可能同时取确定值。反之,如果两个算符不对易,则必存在一些态不是它们共同本征函数,这就意味着在这些态上它们不可能同时取确定值。
§4.
6. 1 平均值与差方平均值
1. 平均值
设力学量 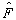 具有分立谱,即
具有分立谱,即
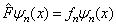 (4.6.1)
(4.6.1)
以
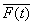 表示力学量
表示力学量  的平均值,
的平均值,
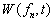 为
为
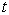 时刻力学量
时刻力学量
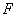 在态中出现的概率。则
在态中出现的概率。则
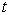 时刻力学量
时刻力学量
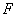 在态中的平均值显然是
在态中的平均值显然是
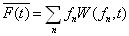 (4.6.2)
(4.6.2)
由线性厄米算符本征函数系的完备性容易证明平均值公式(4.6.2)与下式等价。
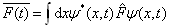 (4.6.3)
(4.6.3)
证明:首先,由(4.6.2)式导出(4.6.3)式。由于
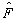 的本征函数系
的本征函数系
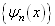 是完备的,所以可将
是完备的,所以可将
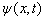 向
向
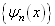 展开
展开
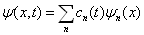 (4.6.4)
(4.6.4)
再把上式代入(4.6.2)式,得
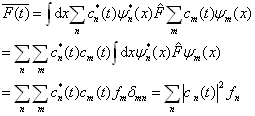 (4.6.5)
(4.6.5)
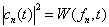 。
(4.6.6)
。
(4.6.6)
(4.6.3)式成立。按着(4.6.5)式的逆向进行,可以由(4.6.3)式导出(4.6.2)式。在不同问题中,有时用(4.6.2)方便,有时用(4.6.3)方便。可归一化的态函数用两者都可以,归一为
 函数的,用
(4.6.2)更方便。例如,求动量在态
函数的,用
(4.6.2)更方便。例如,求动量在态
 ,
,
上的平均值。首先将
 向动量本征函数展开,
向动量本征函数展开,
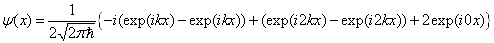 。
。
然后由动量出现的相对概率求出概率,再求出动量平均值,
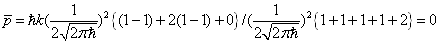 。
。
定义差方平均值为
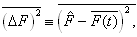 (4.6.7)
(4.6.7)
容易证明
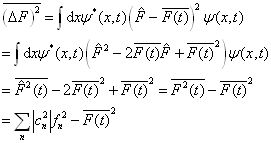 (4.6.8)
(4.6.8)
上式表明,一个力学量的差方平均值等于该力学量算符平方的平均值与平均值平方之差。也可以用均方根误差 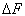 来描述测量误差,它与差方平均值之间的关系为
来描述测量误差,它与差方平均值之间的关系为
 (4.6.9)
(4.6.9)
§4.
6. 2 不确定关系
不确定关系,或说是测不准关系,是经典物理没有,而量子力学才有的一个十分重要的关系式。它是波粒二象性的一个必然结果。为证明不确定关系,先证明施瓦兹(Schwarz)不等式:
 (4.6.10)
(4.6.10)
其中,
 和
和
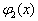 是在任意区域
是在任意区域 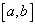 上任意连续态函数,仅当
上任意连续态函数,仅当
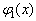 和
和
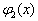 正比时,等号才成立。
正比时,等号才成立。
证明:令 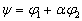 ,则
,则
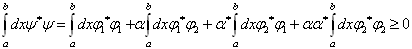 (4.6.11)
(4.6.11)
选择
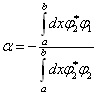 (4.6.12)
(4.6.12)
考虑到  ,得到(4.6.10),证毕。
,得到(4.6.10),证毕。