3.不确定关系的证明
不确定关系可以表述为：同时测量两个线性厄米算符
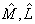对应的力学量，它们的差方平均值满足关系式
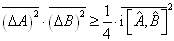(4.6.13)
证明：令
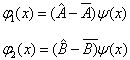(4.6.14)
其中， 
为任一个归一化的波函数。
由施瓦兹不等式知
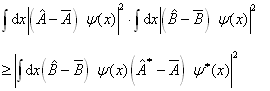(4.6.15)
即
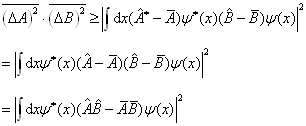(4.6.16)
式中，
(4.6.17)
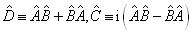(4.6.18)
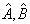为线性厄米算符，则
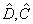也一定是线性厄米算符，因此其平均值
必为实数。将(4.6.17)式代入(4.6.16)式，得到
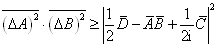(4.6.20)
由于，
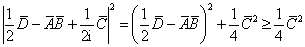(4.6.21)
将上式代入(4.6.20)式，得到
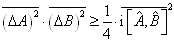(4.6.22)
此即算符 
与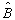 
的不确定关系式。
应强调指出，
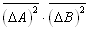不仅仅与对易关系
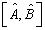有关，而且与所处状态有关，尽管
，但在某些态上仍可能有
，即，这种情况下，力学量 、 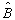虽不对易，仍可能同时有确定值。仅当
时，
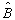、 才在任何态上都不能同时有确定值，例如
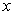和
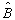就是这种情况。更详细一点说， 、 不对易，但同时有唯一确定值的必要条件是，对易子
是有零本征值的非常数算符，且对易子
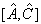与
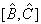为零或者有零本征值。这是因为，若
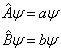(4.6.23)
则
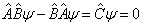(4.6.24)
可见，
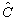必须是有零本征值的算符，相应的本征函数为 
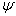。并且必有
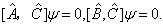
综上所述可见，当且仅当两个算符对易时，它们存在共同完备的本征函数系；而当两个算符不对易时，它们虽然可能有共同本征函数，但这些共同本征函数必然不能构成共同完备本征函数系。