§4
问题讨论：关于一个对易关系的讨论
一个由两个一维粒子组成的体系，其算符相对坐标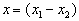 
与总动量
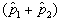是对易的，即
。
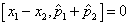这意味着
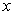与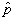 
有共同的本征态，其本征值可取
或
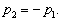
有的文献认为这难以理解。‘这是多么奇怪的态，两个以相反动量方向运动的粒子居然可以保持它们之间的距离不变！简直不可思议。’
‘谁也想不出怎样实现这种……运动，难怪好多人把Einstein同Bohr之间的争论只当作是一场不会有结果得空谈。’
我们认为，实际上并非如此。首先我们考虑在动量本征态中的一维粒子的运动。
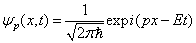
显然，
时刻粒子在空间各处的概率是相同的，皆为
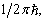
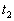时刻粒子在空间各处的概率仍然是是相同的，仍然皆为
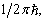，粒子位置的概率没有发生变化。这说明，在量子力学中，不能由粒子动量不为零就断言粒子位置的概率。对于一个处于单色波的粒子说来，无论其动量多大，任何时刻其在空间的概率都相同都是
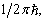。同理，不能由两个粒子相对动量不为零就断言两个粒子相对位置的概率必然要发生变化。实际上，粒子位置，或两个粒子相对位置，的概率的变化决定于粒子波包的色散关系。一个粒子系中，各粒子间相对位置和总动量同时有确定值是容易理解的，也是必要的。只有这样，只有粒子系中各粒子间的相对位置不变，这些粒子才可能构成定域于有限空间范围内的粒子系。