§4.
1. 1 算符及其运算规则
1．线性算符
任一个能将一个函数变为另一个函数的变换，例如，数字2、复共轭、开方、积分都是算符。但在量子力学中，由于状态叠加原理成立，可观测量对应的算符都必是线性算符。所谓线性算符是指满足下列运算规则的算符，
，
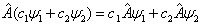(4.1.1)
其中，
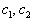是两个任意复常数，
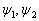是两个任意的波函数。
2．算符相等
如果两个算符
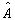和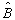 
对体系的任一波函数 
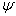的作用都相同，
，
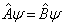则称两个算符
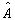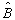和 相等，记为
。
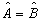定理1
若算符
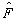对任意波函数
都有
，
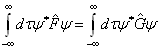(4.1.2)
则.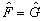 
。
证明
定理的必要性是显然的。下面证明其充分性。任取.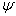 
和.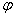 
，由条件可得
，
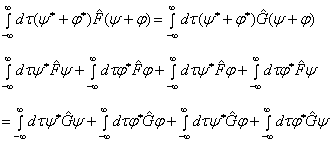(4.1.3)
由于
，
得到
。
(4.1.4)
令
，(4.1.4)变为
。
(4.1.5)
(4.1.4)+
(4.1.5)得
(4.1.6)
因为
是任意的，所以
，即
。
3．单位算符
若对任意的波函数 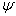，算符
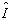满足
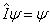(4.1.7)
则称
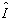为单位算符。显然，任意波函数皆为单位算符的本征态，且本征值为1。
4．算符之和
若对任意的波函数 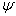，下式
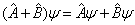(4.1.8)
总是成立，则称算符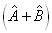 
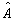为算符 
与算符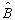 
之和。算符的加法运算满足交换律和结合律，即
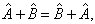
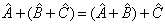(4.1.9)