5.算符之积
两个算符 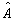 和
和 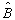 之积记为
之积记为 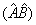 ,对任意的波函数
,对任意的波函数 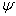 ,算符
,算符
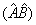 的作用定义为下列运算
的作用定义为下列运算
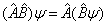 。
(4.1.10)
。
(4.1.10)
即算符之积
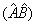 对任意波函数的运算过程是,先用算符
对任意波函数的运算过程是,先用算符 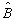 对
对
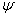 进行运算,得到一个新的波函数(
进行运算,得到一个新的波函数( 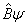 ),然后,再用算符
),然后,再用算符
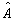 对(
对(
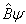 )进行运算。
)进行运算。
一般情况下,
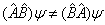 ,
,
即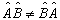 (4.1.11)
(4.1.11)
可见,算符运算与普通代数运算有重要 差别。
6.
算符之逆
设由算符方程
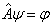
能够惟一地解出 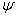 ,则可定义算符
,则可定义算符 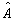 的逆算符
的逆算符
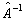 为
为
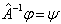 (4.1.13)
(4.1.13)
应该说明的是,并非所有的算符都具有相应的逆算符。若算符
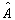 的逆算符
的逆算符
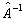 存在,则有
存在,则有
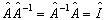 (4.1.14)
(4.1.14)
设算符
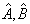 的逆都存在,容易证明
的逆都存在,容易证明
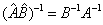 (4.1.15)
(4.1.15)
7.转置算符
对任意的波函数
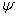 和
和 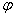 ,算符
,算符 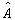 的转置算符
的转置算符 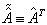 满足
满足
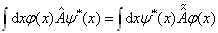 (4.1.16)
(4.1.16)
例如,试求
![]() 由定义
由定义
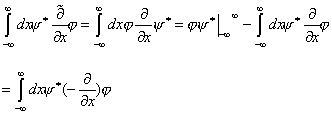 (4.1.17)
(4.1.17)
由此得
![]() 。
(4.1.18)
。
(4.1.18)
这里用了![]() 时,
时,![]() 的条件。根据算符转置的定义,有
的条件。根据算符转置的定义,有
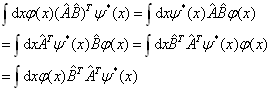 (4.1.19)
(4.1.19)
即,
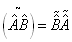 (4.1.20)
(4.1.20)