8．复共轭算符与厄米共轭算符
算符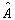 
的复共轭算符 
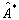是将
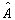中的所有复量换成共轭复量，即虚数
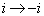。例如，动量的 
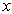分量算符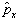 
的复共轭算符
。
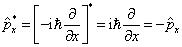(4.1.21)
算符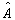 
的厄米共轭（简称为共轭）算符 
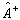定义为，对任意的波函数
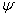和 
，
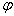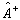满足
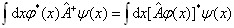(4.1.22)
由转置算符的定义知
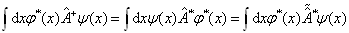(4.1.23)
于是，有
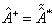(4.1.24)
即一个算符的厄米共轭为此算符转置后再取其复共轭。例如由(4.1.18)和(4.1.21)，可得
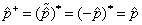(4.1.25)
容易证明
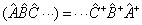(4.1.26)
9．厄米算符
若算符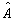 
满足
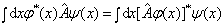(4.1.27)
则称算符
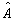为厄米算符。由厄米共轭算符的定义可知，厄米算符满足
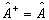(4.1.28)
这样，厄米算符也称之为自共轭算符。例如算符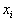 
、 
、 
、 
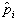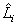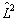都是厄米算符。
容易证明，两个厄米算符之和仍是厄米算符，而它们的积一般不再是厄米算符，除非它们是对易的，因为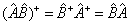 
；
10．幺正算符
如果算符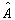 
满足
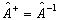(4.1.29)
则称之为幺正算符。
11．算符函数
若函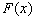数 
的各阶导数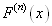 
均存在，且对其作幂级数展开时是收敛的，即
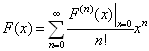(4.1.30)
则对应算符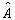 
的算符函数 
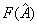为
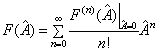(4.1.31)