§4.
1. 2 对易关系
1. 对易关系
为了描述两个算符
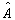与
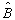之积的交换关系，定义
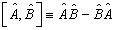(4.1.32)
为算符
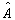与
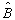的对易关系。如果
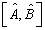＝0，则称算符
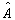与
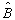是可对易的，否则，称
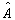与
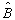是不对易的。根据所研究的的不同，有时要用到两个算符
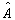与
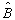的反对易关系，其定义为
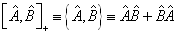(4.1.33)
2.
对易关系的计算
（1）、对于最基本的对易关系，通过定义直接计算。
例1.
计算对易子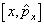 
。
解:
对于任意的状态
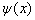，有
由于
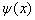是一个任意的状态，所以，
。
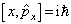类似地，容易得到，
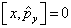。由此，有
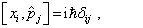(4.1.36)
此即著名的海森堡对易关系，它是量子力学中最基本的对易关系。此外，容易证明
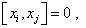(4.1.37)
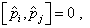(4.1.38)
§4
练习1
对易关系的例题
例1.
计算对易子
。
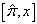解:
对于任意的状态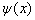，有
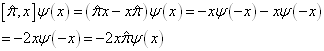
所以，
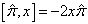(4.1.1)
或者，
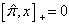(4.1.2)
例2.
计算对易子
。
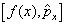解:
对于任意的状态
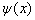，有
，
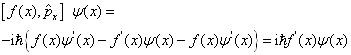所以，
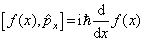(4.1.3)
（2）、利用对易关系的运算规则计算。
对易子代数的运算规则如下：
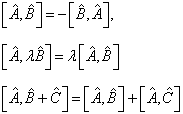(4.1.39)
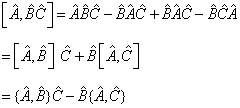(4.1.40)
式中，
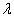为常数。