设
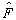 为一个守恒量算符,则
为一个守恒量算符,则
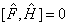 。这时,它们具有完备的共同本征函数系
。这时,它们具有完备的共同本征函数系
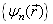 ,
,
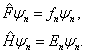 。
(4.7.8)
。
(4.7.8)
且任意一个状态
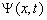 可以展开为
可以展开为
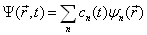 (4.7.9)
(4.7.9)
其中,
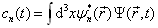 (4.7.10)
(4.7.10)
将上式两端对时间作微商
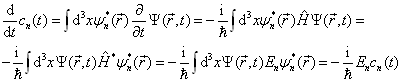 (4.7.11)
(4.7.11)
对上式作积分,得到
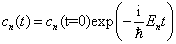 (4.7.12)
(4.7.12)
在任意时刻 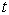 ,力学量
,力学量 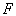 在
在
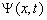 上取
上取
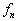 值的几率为
值的几率为
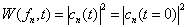 (4.7.13)
(4.7.13)
可见,当算符
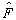 与哈密顿算符
与哈密顿算符
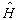 相互对易时,无论是否在定态,守恒量
相互对易时,无论是否在定态,守恒量 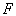 的取值几率都不随时间改变。另外,将(4.7.12)式代入(4.7.9)式,得到一个计算
的取值几率都不随时间改变。另外,将(4.7.12)式代入(4.7.9)式,得到一个计算
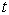 时刻波函数的公式
时刻波函数的公式
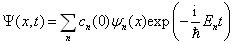 (4.7.14)
(4.7.14)
利用它可以方便地由 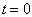 时的波函数求出任意时刻
时的波函数求出任意时刻 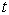 的波函数。
的波函数。
如果状态是简并的,上述结论也是正确的。
定态
设
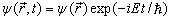 为一定态,
为一定态,
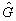 为任意线性厄米算符。已经知道,
为任意线性厄米算符。已经知道,
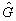 在定态上的平均值是不变的。现在证明,与时间无关的算符
在定态上的平均值是不变的。现在证明,与时间无关的算符
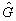 的任一本征值
的任一本征值
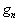 出现的概率
出现的概率
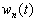 也是不变的。
也是不变的。
设
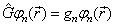 ,则
,则
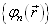 是完备的。因此有
是完备的。因此有
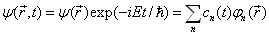 ,
,
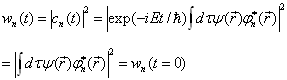 。
。
可见,在定态,无论算符
 是否为守恒量算符(
是否为守恒量算符( 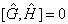 ),其本征值出现的概率都不变。
),其本征值出现的概率都不变。
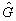 又非守恒量,则一般说来
又非守恒量,则一般说来
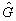 及
及
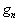 出现的概率
出现的概率
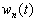 都要随时间变化。
都要随时间变化。