§4深入学习内容:
2.量子力学的基本假设
(参阅
C.Cohen-Tannoudji, B.Diu, F.Laloe 刘家谟
陈星奎
译
量子力学
高教出版社
1984,第三章)
1.体系态的描述
假设1:在确定的时刻  ,一个物理体系的状态由态空间ε中一个特定的右矢
,一个物理体系的状态由态空间ε中一个特定的右矢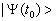 来确定。
来确定。
注意,由于ε是一个矢量空间,因此第一个假定就隐含着叠加原理:若干态矢量的线性组合也是一个态矢量。
2.物理量的描述
假设2:每一个可以测量的物理量A都可以用在ε空间中的一个变换算符 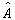 来描述;这个算符是一个线性厄米算符。
来描述;这个算符是一个线性厄米算符。
算符的线性决定了在量子力学中叠加原理成立。这一假设显然与前一假设是自洽的。
3.物理量的测量
假设3::每次测量到的物理量
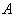 的值,只能是相应的算符
的值,只能是相应的算符
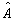 的本征值之一。
的本征值之一。
假设4:对于分立谱的情况,若体系处于已归一化的态 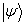 中,则测量物理量
中,则测量物理量
 得到其本征值
得到其本征值 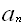 的概率
的概率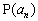 是:
是:
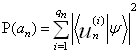 ,
,
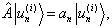

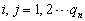 .
.
式中  是
是
 的简并度.
的简并度.
对于非简并连续谱的情况,测量处于已归一化的态 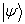 的体系的物理量
的体系的物理量
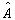 时,
得到介于α和α+dα之间的结果的概率是:
时,
得到介于α和α+dα之间的结果的概率是:
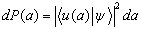 ,
,
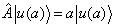 .
.
数学上证明了,如力学量完全集中包含有体系的哈密顿量
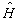 ,而
,而
 本征值又有下确界,则这一组力学量完全集的共同本征态构成这一体系态空间的一组完备基矢(曾谨言,
量子力学,卷1,第三版,
p.233,
科学出版社,2000
)。
本征值又有下确界,则这一组力学量完全集的共同本征态构成这一体系态空间的一组完备基矢(曾谨言,
量子力学,卷1,第三版,
p.233,
科学出版社,2000
)。
由上述假设容易从物理上理解这一结果(不失一般性,这里仅讨论无简并分立谱情况)。由假定2和3可知,对任一个确定的状态测量物理量
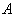 都必将给出
都必将给出
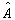 的各个本征值出现的概率幅,本征值谱之外的任何值都不可能出现;反之,如果给定了
的各个本征值出现的概率幅,本征值谱之外的任何值都不可能出现;反之,如果给定了  (更确切地说是包含
(更确切地说是包含  的力学量完全集,从而力学量完全集本征值组决定的本征矢无简并)的每个本征值的概率幅,那也就完全确定了一个状态。这就意味着任一状态波函数都必然能够用
的力学量完全集,从而力学量完全集本征值组决定的本征矢无简并)的每个本征值的概率幅,那也就完全确定了一个状态。这就意味着任一状态波函数都必然能够用
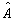 的本征函数展开,也就是说
的本征函数展开,也就是说  的本征函数构成了完备本征函数系。如果某一态不能用这组基展开,那就意味着还需要新的线性独立本征矢,从而就要有新的本征值(因为无简并)。新的本征值如果不在原本征值谱中,按假设3,则是不可测的,因而不可能。这样,任一态函数
的本征函数构成了完备本征函数系。如果某一态不能用这组基展开,那就意味着还需要新的线性独立本征矢,从而就要有新的本征值(因为无简并)。新的本征值如果不在原本征值谱中,按假设3,则是不可测的,因而不可能。这样,任一态函数
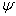 都可以向一组力学量完全集的本征函数系
都可以向一组力学量完全集的本征函数系
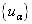 展开,相应的展开系数
展开,相应的展开系数
 就是力学量完全集中各力学量本征值出现的概率幅
就是力学量完全集中各力学量本征值出现的概率幅  ,
,
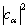 是相应的概率。
是相应的概率。