§4
练习2
是否为厄米算符的通常判别方法
1、利用厄米算符的定义直接进行判别
例1
证明动量
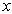分量算符
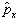是厄米算符。
证明：
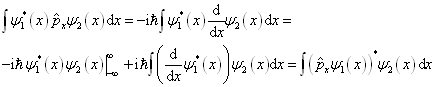(4'.1.4)
上式最后一步成立是有条件的：要求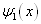 
和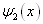 
中至少有一个满足在无穷远处为零的条件。如果
和
两者皆不满足在无穷远处为零的条件，那么，考虑都是单色平面波的情况，即
(4'.1.5)
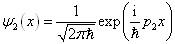(4'.1.6)
分别计算
与
，
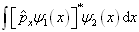得到
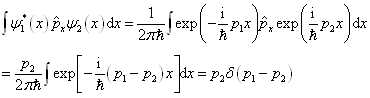(4'.1.7)
(4'.1.8)
利用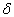 
函数的性质
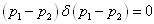(4'.1.9)
可知
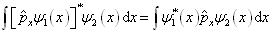(4'.1.10)
说明即使
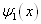和
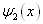两者都是单色平面波，算符
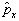也是厄米算符。对于
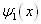和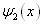 
都是有限单色平面波组合的情况同样可以证明
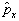是厄米算符。同理可以证明算符
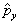与
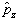也是厄米算符。
可以证明，实函数算符必为厄米算符；两个厄米算符之和仍为厄米算符。但是对于两个厄米算符的乘积，容易证明当且仅当它们彼此对易时，它们之积才是厄米算符。
2、利用自共轭条件来判断
例3
算符
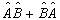与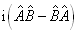 
是厄米算符。
证明：
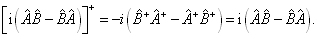
另外，任意线性算符
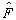总可以写成两个厄米算符的组合
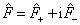(4'.1.11)
其中厄米算符
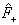与
分别为
；
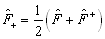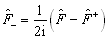(4'.1.12)