2．有简并的情况
当有简并时，
，
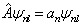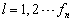。如果没有其它条件，这
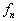个简并的波函数的选择并不是惟一的，一般来说，它们也不一定是正交的。但是，总可以把它们重新线性组合，使之满足正交归一化条件。为此，利用
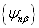构造一组新的波函数
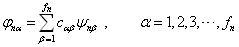(4.2.7)
再用算符
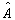从左作用上式两端，得
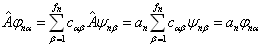(4.2.8)
说明
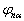仍然是算符
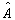的属于本征值
的本征波函数。选择系数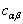 
使
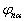具有正交、归一性，即
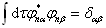(4.2.9)
由于，系数 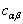的个数为
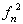，而满足的条件数为
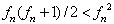，即待定系数个大于方程的个数，所以，方程必有解，且有多组解。
利用施密特（Schmidt）方法可以将一组波函数化为正交归一化的波函数。施密特正交归一化方法的基本步骤是：
首先，选取一个态矢，例如，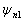 
，求出其归一化的表示
(4.2.10)
其次，构造
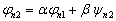(4.2.11)
利用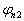 
与 
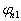正交的要求
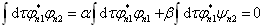(4.2.12)
得到
(4.2.13)
此外，还要求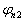 
是归一化的，即
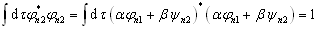(4.2.14)
于是可以求出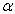 
和 
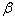，进而得到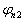 
。
然后，再构造
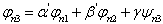(4.2.15)
利用其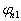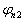与 、 与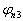 
的正交条件及归一化条件确定 
、 
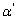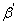和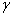 
，如此做下去，直至将全部本征矢变换完毕，则 
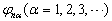就是已经正交归一化的简并波函数。
这样，简并本征态的正交归一化条件为
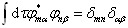(4.2.16)
当有简并时，就意味着仅这一个算符不能将态完全确定下来，必须引入另外的算符才能将态完全确定下来（即后面要讲到的力学量完全集）。这些算符的共同本征函数自动满足正交性。