§5.5
常用表象及其变换
在量子力学中，坐标、动量和能量表象是常用的表象。其中坐标和动量表象是连续谱表象，与束缚态有关的能量表象为分立谱表象。不失一般性，下面以一维问题为例说明有关表象。
1．
坐标表象
算符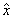 
的本征值为 
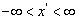。考虑到
，
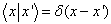在自身表象中，
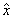的矩阵元为
，
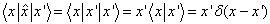(5.5.1)
这里 
是行指标， 
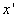是列指标。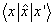 
是对角矩阵。
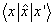对波函数（一列矩阵）的作用（矩阵相乘，求和化为积分）是
。
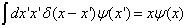(5.5.2)
可见，在自身表象中，
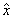对波函数的作用简化为用其本征值乘这个态矢相应的分量，正如我们所熟悉的那样。这个性质对于其它力学量表象也成立，因为力学量在其自身表象中必是对角的。
坐标表象中动量算符的矩阵元是
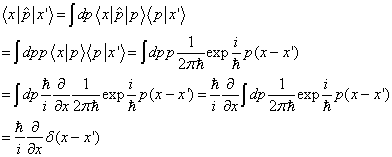(5.5.3)
这一算符对波函数作用为
。
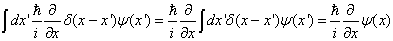(5.5.4)
即，在坐标表象中，动量算符对波函数作用简化为对波函数的微商。
在坐标表象中，作为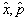 
函数的算符的矩阵形式可由
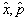的矩阵相乘得到。例如
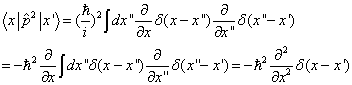(5.5.5)
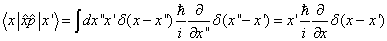(5.5.6)
由狄拉克符号形式的薛定锷方程导出坐标表象的薛定锷方程
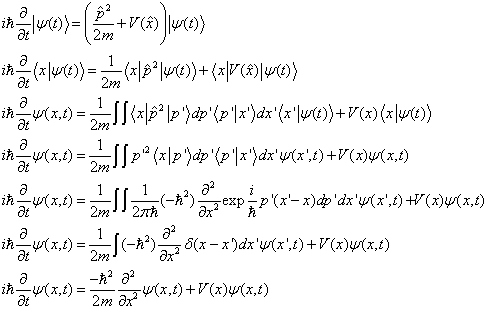(5.5.7)
推导中用到了动量本征矢在坐标表象中的波函数
；
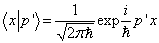动能算符在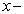 
表象中的矩阵形式是
，
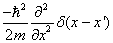(5.5.8)
推导中将其作用于波函数，即完成对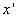 
的积分后（相当于完成矩阵乘法），就得到了熟悉的动能算符在
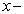表象中的微商形式
。
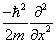