例题5.1
已知体系的哈密顿算符  和力学量算符
和力学量算符
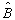 的矩阵形式分别为
的矩阵形式分别为
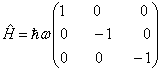
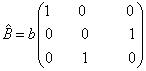
其中, 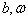 为实常数。证明
为实常数。证明
 与
与
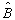 都是厄米算符,并且互相对易。求出它们的共同本征函数系。
都是厄米算符,并且互相对易。求出它们的共同本征函数系。
解:由厄米算符的定义知,厄米算符
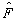 满足
满足
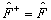 (1)
(1)
或者
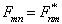 (2)
(2)
题中所给出的哈密顿算符
 和力学量算符
和力学量算符 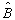 皆为实对称矩阵,故它们都是厄米算符。
皆为实对称矩阵,故它们都是厄米算符。
因为
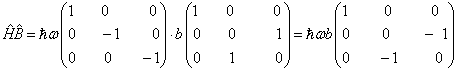 (3)
(3)
而
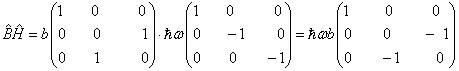 (4)
(4)
所以,有
 (5)
(5)
设
 满足的本征方程为
满足的本征方程为
 (6)
(6)
由于
 是对角矩阵,所以,它是在自身表象中给出的,它的本征值就是其对角元,即
是对角矩阵,所以,它是在自身表象中给出的,它的本征值就是其对角元,即
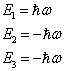 (7)
(7)
其中, 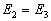 ,能量具有二度简并。由于简并的存在,仅由算符
,能量具有二度简并。由于简并的存在,仅由算符
 不能惟一确定
不能惟一确定 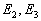 的波函数。
的波函数。
当
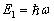 时,波函数满足
时,波函数满足
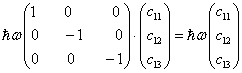 (8)
(8)
显然,
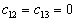 (9)
(9)
于是,考虑到归一化的波函数为
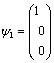 (10)
(10)
当 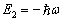 时,波函数满足
时,波函数满足
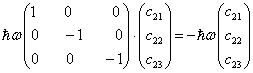 (11)
(11)
得到
 (12)
(12)
相应的波函数为
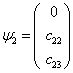 (13)
(13)
同理可知, 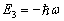 的波函数为
的波函数为
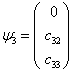 (14)
(14)