利用归一化条件可知
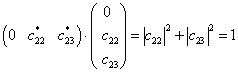 (15)
(15)
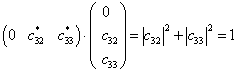 (16)
(16)
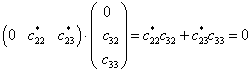 (17)
(17)
由于头两个正交条件给不出任何信息,所以,8个变量满足四个方程,不能惟一的定出这8个常数。这就是能量简并时波函数不能惟一确定的原因。
将 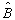 作用于
作用于 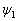 得
得
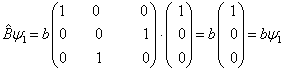 (18)
(18)
上式说明
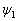 也是算符
也是算符 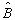 的本征函数,对应的本征值为
的本征函数,对应的本征值为 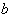 。
。
当
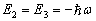 时,波函数
时,波函数 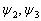 无法惟一确定,它们的矩阵形式是一样的,为简洁计,统一记为
无法惟一确定,它们的矩阵形式是一样的,为简洁计,统一记为
 (19)
(19)
用算符
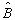 作用上式,得到本征值满足的本征方程
作用上式,得到本征值满足的本征方程
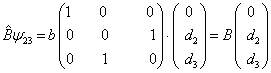 (20)
(20)
在简并子空间中,久期方程为
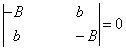 (21)
(21)
得到 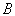 的另外两个本征值,分别记为
的另外两个本征值,分别记为
 (22)
(22)
当 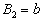 时,将其代入(24)式,有
时,将其代入(24)式,有
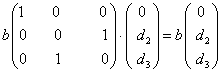 (23)
(23)
得到
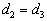 (24)
(24)
由归一化条件知
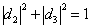 (25)
(25)
进而,得到
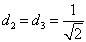 (26)
(26)
将其代入(19)式,有
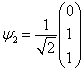 (27)
(27)
当 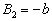 时,重复上面的求解过程,可以得到
时,重复上面的求解过程,可以得到
 (28)
(28)
(27)及(28)中的矩阵元显然满足(15)-(17),或直接代入也可知,(27)及(28)是 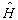 的本征值为-1的本征函数。可见,引入算符
的本征值为-1的本征函数。可见,引入算符
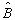 后,消除了
后,消除了  的本征函数的二度简并。
的本征函数的二度简并。