§5.1.2
波函数表象
以一维问题为例,设 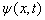 是坐标表象中的任意一个归一化的波函数。下面导出这一状态
是坐标表象中的任意一个归一化的波函数。下面导出这一状态  分别在坐标、动量及任意力学量
分别在坐标、动量及任意力学量
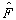 表象中的表示。
表象中的表示。
1、波函数在力学量![]() 表象中的表示
表象中的表示
如上所述,所谓状态波函数在任意力学量 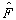 表象中的表示就是给出力学量
表象中的表示就是给出力学量
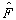 的本征值
的本征值![]() 出现的概率幅。
出现的概率幅。 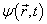 是
是![]() 时刻力学量
时刻力学量 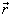 出现的概率幅,所以
出现的概率幅,所以 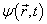 就是状态波函数在
就是状态波函数在![]() 中的表象,也是迄今为止我们最熟悉的表象。下面我们由此表象求出此状态在任意力学量
中的表象,也是迄今为止我们最熟悉的表象。下面我们由此表象求出此状态在任意力学量
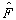 中的表象。首先要求解
中的表象。首先要求解
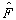 本征方程,
本征方程,
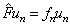 。
(5.1.1)
。
(5.1.1)
由此得到本征值谱
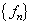 和正交归一的本征矢集
和正交归一的本征矢集![]() 。由于
。由于![]() 是完备的,体系任一状态矢量
是完备的,体系任一状态矢量
 都可以用此完备集展开(设
都可以用此完备集展开(设 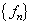 是分立的)。
是分立的)。
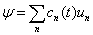 , (5.1.2)
, (5.1.2)
并且有
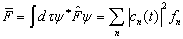 。
(5.1.3)
。
(5.1.3)
可见  就是
就是 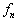 在态
在态![]() 中出现的概率幅,
中出现的概率幅,
 确定,则此状态就完全确定。将
确定,则此状态就完全确定。将  按
按 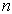 顺序排成一列矩阵,就得到了状态波函数在
顺序排成一列矩阵,就得到了状态波函数在
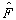 表象中的表示
表象中的表示
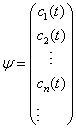 。
(5.1.4)
。
(5.1.4)
这时,两个态矢量的内积可写为
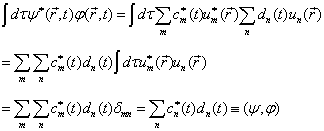 (5.1.5)
(5.1.5)
这里我们引用了一个表示两个波矢量内积的记号
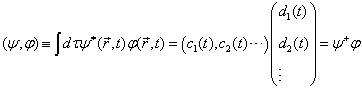 。
(5.1.6)
。
(5.1.6)
如果
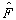 的本征值是连续谱
的本征值是连续谱 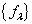 ,则对本征值谱的求和要化为积分,并且只能想象
,则对本征值谱的求和要化为积分,并且只能想象
 是一列矩阵,而不能写出。如果
是一列矩阵,而不能写出。如果  在坐标表象中是归一化的,则在
在坐标表象中是归一化的,则在
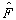 表象中也是归一化的。即,
表象中也是归一化的。即,
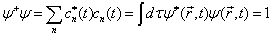 。
(5.1.7)
。
(5.1.7)
如果  是一组力学量完备集的共同本征矢,则其下标要用多个指标。
是一组力学量完备集的共同本征矢,则其下标要用多个指标。
这里是由我们熟悉的坐标表象导出任一力学量
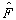 的表象,但这不是必须的。各种表象都是等同的。我们也可能先得到其它某一力学量表象,再由这一力学量表象导出(通过么正变换)坐标表象。
的表象,但这不是必须的。各种表象都是等同的。我们也可能先得到其它某一力学量表象,再由这一力学量表象导出(通过么正变换)坐标表象。