§5.2
力学量算符的矩阵表示
§5.2.1
力学量算符的矩阵表示
算符是对波函数的变换,因此当波函数表象改变时,算符的形式也必然随之发生相应的变换。我们还是从熟悉的坐标表象中的算符形式导出在其它力学量表象中的算符形式。设在坐标表象中已知:
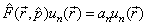 ,
(5.2.1)
,
(5.2.1)
 ,
(5.2.2)
,
(5.2.2)
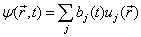 ,
,
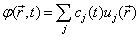 ,
(5.2.3)
,
(5.2.3)
这里 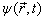 是任意态矢量。现在求算符
是任意态矢量。现在求算符 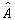 在力学量
在力学量 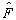 表象中的形式。以
表象中的形式。以 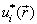 乘(5.2.2)两边并积分,利用(5.2.3),得
乘(5.2.2)两边并积分,利用(5.2.3),得
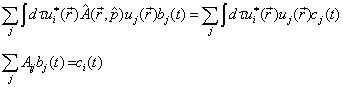 (5.2.4)
(5.2.4)
这里用了
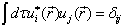 ,
,
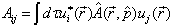 。
(5.2.5)
。
(5.2.5)
由(5.2.5)可见, 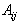 只决定于算符
只决定于算符 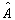 及
及 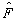 的本征矢
的本征矢 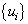 。由
。由
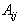 按脚标顺序排列就构成了一个方矩阵,
按脚标顺序排列就构成了一个方矩阵,
 。
(5.2.6)
。
(5.2.6)
这个矩阵就是算符
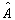 在力学量
在力学量 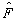 表象中的表示。
表象中的表示。
量子力学中的力学量算符是厄米的。在
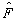 表象中,若算符
表象中,若算符 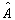 的矩阵元由(5.2.5)式定义,则其复共轭为
的矩阵元由(5.2.5)式定义,则其复共轭为
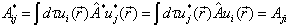 (5.2.7)
(5.2.7)
即
 。
(5.2.8)
。
(5.2.8)
满足(5.2.8)的矩阵称为厄米矩阵。可见,厄米算符对应的是厄米矩阵。如同厄米算符的本征值一样,厄米矩阵的本征值是实数。
再来考虑一种特殊的算符矩阵,即力学量算符在自身表象中的矩阵,根据定义可知
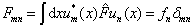 (5.2.9)
(5.2.9)
写成矩阵形式为
 (5.2.10)
(5.2.10)
可见,算符在自身表象中是一个对角矩阵,并且,本征值就是其对角元。这一矩阵的迹 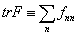 就是全部本征值之和。
就是全部本征值之和。
一般将坐标表象中的量子力学称之为波动力学,把任意力学量表象中的量子力学表示称之为矩阵力学。狄拉克证明了它们是等价的。