§5.2.2
量子力学公式的矩阵表示
1、
算符方程
由(5.2.4)可以看出，算符方程(5.2.2)可以写成矩阵形式
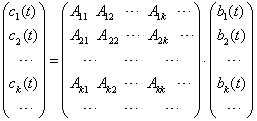(5.2.11)
2、
本征方程
算符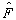 
的本征方程是算符方程的一个特例，用完全类似的方法可以写出算符本征方程的矩阵形式。在
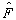表象之下，算符 
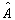本征方程的矩阵形式为
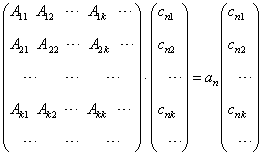(5.2.12)
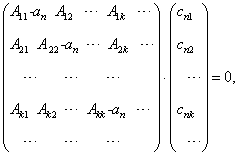(5.2.13)
线性齐次方程有解的条件是其系数行列式为零，即
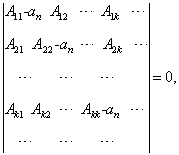(5.2.14)
如果这行列式是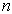 
阶方阵，则这是一个关于本征值 
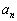的 
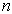次方程。最多有 
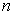个不同实根，这些根就是算符
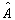的本征值。将各个依次代入方程(5.2.13)，在考虑到归一化条件，就得到了在 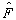－表象中的与各个本征值相应的本征函数。因为任意力学量在自身表象中的矩阵都是对角的，所以，通常把求解本征方程的过程称为算符矩阵的对角化的过程。
3、
薛定谔方程
注意到当力学量算符不含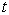 
时，其本征函数也不含
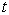。因此本征函数与 
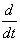可交换。这样，用导出(5.2.11)相似的步骤可得薛定諤方程的矩阵形式
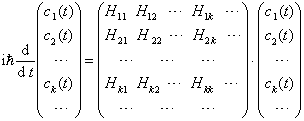(5.2.15)
4、
平均值公式
计算任意厄米算符
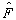在状态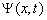 
上的平均值公式为
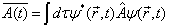(5.2.16)
在
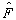表象中，有
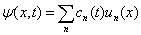(5.2.17)
把上式代入(5.2.16)式，得到
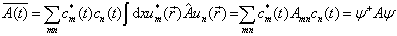， (5.2.18)
即，
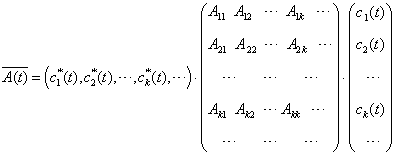(5.2.19)
综上所述，同样一个物理问题可以在不同的表象下处理，尽管在不同的表象下，波函数及算符的矩阵元是不同的，而最后所得到的物理结果（力学量的可能取值、取值几率和平均值）却都是一样的。所以，允许对表象作选择。如果选取了一个合适的表象，将使问题得到简化。这也就是表象理论的价值所在。