§5。3
狄拉克符号
§5.3.1
左矢(bra)和右矢(ket)
我们知道，矢量之间的内在关系，例如两个矢量的内积或叉乘，不是必须用坐标系才能表达。很多情况下，不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中，一个体系的任一个状态波函数 
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量 
表象时，就相当于选定这个希尔伯特空间的一个坐标系。
的本征矢
就是这个希尔伯特空间的基。态矢量在各个基上的分量 
就组成了这个状态在
表象时的状态波函数（一个列矩阵）。态矢量在一个基
上的分量 
就是这个基相应的本征值
出现的概率幅，
是 
与 
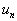的内积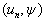 
。由这些可见，作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样，用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克（Dirac）构造的狄拉克符号方法（bra及ket是单词bracket的分拆）。其优点是，由于与具体表象无关，所以运算简洁。
实际上，在讨论表象理论时，一开始用狄拉克符号方法就能够很方便简洁地导出态矢量、算符的表象及表象的变换，而不是必须从坐标表象开始。前面从坐标表象开始，仅仅是为了理解方便。
狄拉克符号是将一个体系中的任一个态矢量
用相应的一个所谓右矢 
来表示。这里 应理解为与具体表象有关的波函数，而写为 时就是与具体表象无关的右矢量，二者有对应关系，但绝不相等，因为 是一个与具体表象无关的抽象的态矢量，而 是与具体表象有关的态矢量，是 的具体表达式。由于态矢量满足叠加原理，相应的右矢也满足叠加原理，因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积，
。
(5.3.1)
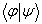是一个复数。对于归一化的右矢， 
。设
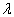为任一复数，由上式得到
。
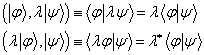(5.3.2)
， 当且仅当
， 
。
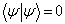(5.3.3)
(5.3.4)
式中，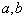 
为任意常数； 若 
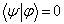，则称
与
两个态矢是相互正交的。