§5.3.2
狄拉克符号在具体表象中的表示
1、封闭性关系
设力学量 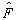 的正交归一完备本征矢为
的正交归一完备本征矢为 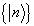 ,则在
,则在
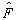 表象中,任意态矢
表象中,任意态矢
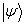 可以向
可以向
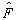 的本征矢展开
的本征矢展开
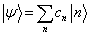 (5.3.5)
(5.3.5)
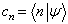 (5.3.6)
(5.3.6)
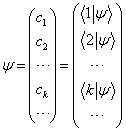 (5.3.7)
(5.3.7)
就是态矢
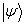 在
在 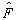 表象中的波函数。 将
表象中的波函数。 将 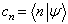 代入(5.3.5)式,有
代入(5.3.5)式,有
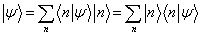 (5.3.8)
(5.3.8)
因为态矢
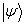 是任意的,且其与求和无关,所以必有
是任意的,且其与求和无关,所以必有
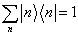 。
(5.3.9)
。
(5.3.9)
对于连续谱,则求和化为积分。例如,坐标和动量表象下的封闭关系分别为
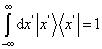 (5.3.10)
(5.3.10)
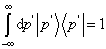 (5.3.11)
(5.3.11)
这一关系相应于厄米算符本征函数的完备性,称为基矢
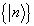 封闭性关系。这是一个非常有使用价值的公式。例如,容易利用这一公式求出两个态矢在一个具体表象中的计算公式。在上述的
封闭性关系。这是一个非常有使用价值的公式。例如,容易利用这一公式求出两个态矢在一个具体表象中的计算公式。在上述的
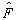 表象中,两个态矢
表象中,两个态矢 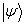 与
与 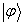 的标积为
的标积为
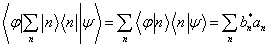 (5.3.12)
(5.3.12)
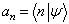 (5.3.13)
(5.3.13)
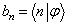 (5.3.14)
(5.3.14)
分别为波函数
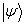 与
与 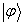 在
在 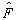 表象中的第
表象中的第 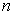 个分量。
个分量。
若取 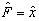 ,则有
,则有
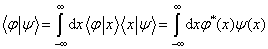 (5.3.15)
(5.3.15)
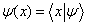 ,
,
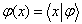 。
(5.3.16)
。
(5.3.16)
设
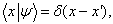
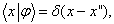 则得到
则得到
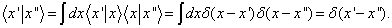 (5.3.17)
(5.3.17)
类似的有
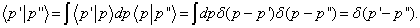 (5.3.18)
(5.3.18)
2、由狄拉克符号过渡到具体表象
设算符 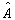 的作用是将态矢
的作用是将态矢
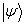 变成态矢
变成态矢
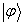 ,
,
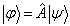 ,
(5.3.19)
,
(5.3.19)
,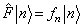
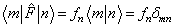 。
(5.3.20)
。
(5.3.20)
(5.3.19)式中的算符及态矢量都是与任何表象无关的、抽象的算符及态矢量。因而以下表达方式都是错误的。