§5 练习
以下表达式是否正确?写出相应的正确表达式。
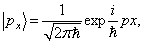
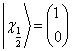 。
。
解:这些表达方式都是错误的。因为左边是与具体表象无关的抽象的态矢量,右边是分别与具体的坐标表象及 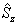 表象有关的具体态矢量,不能相等。实际上,
表象有关的具体态矢量,不能相等。实际上,
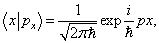
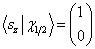 。
。
由抽象的狄拉克符号形式得到具体表象,对于态说来就是要给出这个态矢量 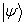 在所给基底
在所给基底  上的分量
上的分量 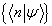 ,
,
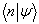 的物理意义是,在所给态上,
的物理意义是,在所给态上, 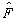 的本征值
的本征值 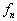 出现的概率幅,因而由
出现的概率幅,因而由  构成的一列矩阵也就是波函数;对于算符说来就是要给出这个算符
构成的一列矩阵也就是波函数;对于算符说来就是要给出这个算符 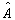 在所给基底
在所给基底 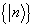 上的矩阵元
上的矩阵元 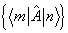 ,由
,由 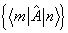 构成的矩阵就是在
构成的矩阵就是在
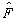 表象中算符
表象中算符 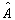 的矩阵形式。由(5.3.20)可见,任一算符在自身表象中,必是对角的,且对角元就是其本征值。因而,只要我们确定了某一个算符的所有本征值,那么只要将这些本征值按一定顺序排列在对角线上,就得到了这一算符在自身表象中的矩阵形式。按这种理解,我们立即能给出在能量表象中,一位谐振子的能量算符矩阵元
的矩阵形式。由(5.3.20)可见,任一算符在自身表象中,必是对角的,且对角元就是其本征值。因而,只要我们确定了某一个算符的所有本征值,那么只要将这些本征值按一定顺序排列在对角线上,就得到了这一算符在自身表象中的矩阵形式。按这种理解,我们立即能给出在能量表象中,一位谐振子的能量算符矩阵元
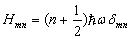 ,
,
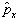 在自身表象中的矩阵元为
在自身表象中的矩阵元为
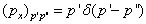 。
。
这样,将(5.3.19)在具体的 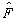 表象中写出就得到
表象中写出就得到
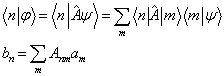 (5.3.21)
(5.3.21)
式中
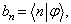
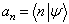 ,
,
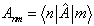 (5.3.22)
(5.3.22)
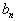 及
及 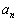 分别是在
分别是在
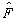 表象中
表象中 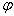 及
及  的矩阵元,
的矩阵元, 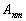 是算符
是算符 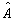 在
在
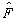 表象中的矩阵元。上式就是算符方程(7.3.19)在
表象中的矩阵元。上式就是算符方程(7.3.19)在
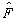 表象中的表示。对于连续谱,求和要化为积分。
表象中的表示。对于连续谱,求和要化为积分。
在
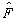 表象下,
表象下,
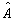 在态矢
在态矢 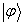 与
与 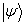 之间的矩阵元
之间的矩阵元 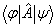 可写为,
可写为,
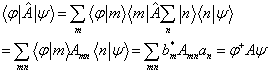 (5.3.23)
(5.3.23)
算符
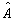 的本征方程
的本征方程
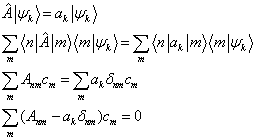 (5.3.24)
(5.3.24)
此即算符
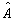 在
在 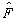 表象下的本征方程,其中,
表象下的本征方程,其中, 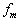 为算符
为算符 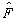 的第
的第 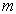 个本征值,
个本征值, 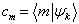 为在
为在 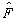 表象下本征值
表象下本征值 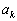 对应的本征矢的
对应的本征矢的 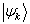 分量。
分量。