第六章
§6.1 中心力场的一般描述
§6.1.1 径向方程
所谓中心力场就是势能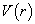 
仅与球坐标的径向坐标 
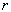有关，而与方向无关，另一方面，在球坐标中
，
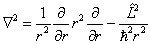(6.1.1)
故
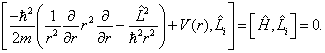
可见，轨道角动量是守恒量。中心力场中的单粒子体系只有三个自由度，所以力学量完备集可选为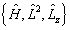 
。
在中心力场中，质量为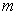 
的粒子满足的定态薛定谔方程是
。
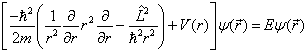(6.1.2)
上式中动能项可看作径向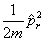动能 
和离心动能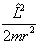 
之和，其中
，
称为径向动量。
(6.1.2)可用分离变量法求解。令
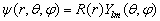(6.1.3)
再将上式代入(6.1.2)式，整理后得到
于是，
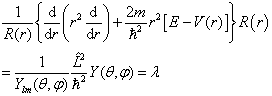(6.1.4)
或写为
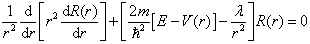(6.1.5)
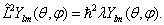(6.1.6)
其中， 
为常数。(6.1.6)的解已经在第4章中给出，本征函数 
就是球谐函数，且
(6.1.7)
由于，(6.1.6)式与势能的形式无关，是中心力场的共同特征，因此，对于一个具体的中心力场而言，只要求解(6.1.5)式即可。。
将(6.1.11)式代入(6.1.9)式，得到
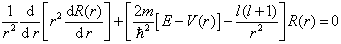(6.1.8)
若令
(6.1.9)
则(6.1.8)式变为
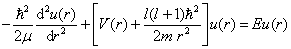(6.1.10)
此即中心力场的径向方程。