§6.1.2
径向方程的讨论
在  处,为了使径向波函数
处,为了使径向波函数  是有限的,
是有限的, 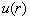 应该满足
应该满足
 (6.1.11)
(6.1.11)
称之为零点条件。
下面讨论 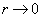 时
时
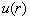 的渐近行为。假设势能满足
的渐近行为。假设势能满足
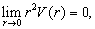
即
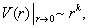
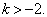 (6.1.12)
(6.1.12)
令
 (6.1.13)
(6.1.13)
则(6.1.10)式变为
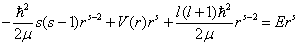 .
(6.1.14)
.
(6.1.14)
将(6.1.12)代入得
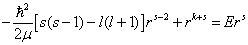 (6.1.15)
(6.1.15)
两端除以 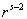 ,考虑到
,考虑到
当 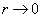 时,
时, 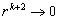 (∵
(∵ 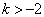 )及
)及
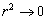 ,
,
得到
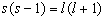 (6.1.16)
(6.1.16)
 的两个根分别为
的两个根分别为
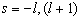 (6.1.17)
(6.1.17)
考虑到(6.1.9),可知,当
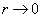 ,方程的两个线性独立解的行为是
,方程的两个线性独立解的行为是
 (6.1.18)
(6.1.18)
考虑解 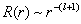 。当
。当
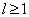 ,
,
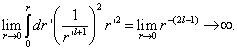 (6.1.19)
(6.1.19)
这破坏了 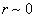 任意邻域内概率有限性要求,因而必须抛弃此解。当
任意邻域内概率有限性要求,因而必须抛弃此解。当 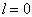 时,
时,
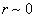 任意邻域内概率有限性要求得以满足,但此时
任意邻域内概率有限性要求得以满足,但此时 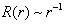 ,
,
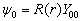 不是方程(6.1.2)的解。因为此时
不是方程(6.1.2)的解。因为此时
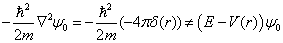 。
。
所以 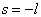 必须抛弃,只有解
必须抛弃,只有解
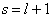 ,
,
即
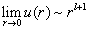 (6.1.20)
(6.1.20)
满足要求。
径向方程(6.1.8)含有角动量量子数 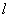 ,但不含磁量子数
,但不含磁量子数 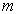 ,因而能量本征值与径向波函数可能与
,因而能量本征值与径向波函数可能与 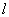 有关,但必不能与磁量子数
有关,但必不能与磁量子数 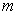 有关。因此能级简并度至少是
有关。因此能级简并度至少是 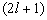 。对于非束缚态,能级是连续的;对于束缚态,能级是分立的。
。对于非束缚态,能级是连续的;对于束缚态,能级是分立的。