§6.2
氢原子
§6.2.1
两体问题化为单体问题
1、两体定态薛定谔方程
氢原子的电子与原子核之间的相互作用库仑势为
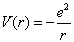 (6.2.1)
(6.2.1)
式中,  为电子与原子核之间的相对距离。
为电子与原子核之间的相对距离。
严格地说,氢原子是一个两体体系,描述这样体系的波函数应该是  ,其中,
,其中, 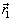 与
与 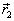 分别是电子和原子核的坐标变量。于是,定态薛定谔方程也要作相应的改变,即
分别是电子和原子核的坐标变量。于是,定态薛定谔方程也要作相应的改变,即
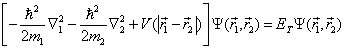 (6.2.2)
(6.2.2)
式中, 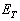 为体系的总能量,
为体系的总能量, 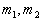 分别为电子与原子核的质量。
分别为电子与原子核的质量。
2、质心坐标与相对坐标的分离
引入质心坐标 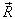 和相对坐标
和相对坐标 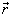
 (6.2.3)
(6.2.3)
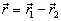 (6.2.4)
(6.2.4)
可以证明,
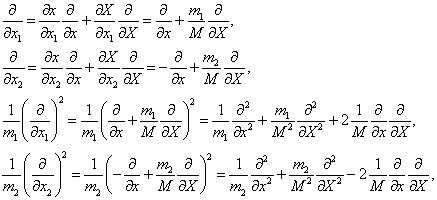 (6'2.1)
(6'2.1)
 (6'2.2)
(6'2.2)
类似地可得到:
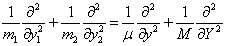 (6'2.3)
(6'2.3)
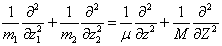 (6'2.4)
(6'2.4)
将(6'2.2)-(6'2.4)相加,得
 )
)
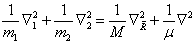 (6.2.5)
(6.2.5)
其中,
 (6.2.6)
(6.2.6)
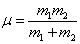 (6.2.7)
(6.2.7)
 是总质量,
是总质量, 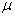 是约化质量(折合质量)。于是,方程(6.2.2)可以改写成
是约化质量(折合质量)。于是,方程(6.2.2)可以改写成
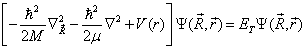 (6.2.8)
(6.2.8)
上式可以分离变量,令
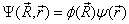 (6.2.9)
(6.2.9)
将其代入(6.2.8)式,得到两个方程
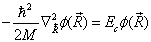 (6.2.10)
(6.2.10)
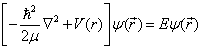 (6.2.11)
(6.2.11)
(6.2.10)式是描述体系质心运动的方程,它是一个自由粒子的波动方程,  是与体系的内部结构无关的质心运动能量。(6.2.11)式是描述体系中电子与原子核相对运动的方程,
是与体系的内部结构无关的质心运动能量。(6.2.11)式是描述体系中电子与原子核相对运动的方程, 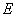 为相对运动的能量。体系的总能量
为相对运动的能量。体系的总能量
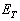 为质心能量
为质心能量  与相对运动能量
与相对运动能量 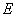 之和。
之和。