角动量相加例题

例2已知两粒子的角动量量子数分别为 。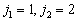

（1）试确定总角动量可能的量子数。

（2）将 态用非耦合表象表出

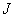解： 可以取值为 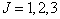，从而可以构成的态是

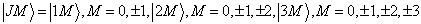          （1）

下面将 态用非耦合表象表出。角动量空间的基底为

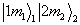
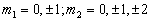                                       （2）

由于 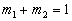（否则C-G系数为零），因此

             （3）

本征方程为 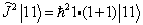，由(7.4.9)得

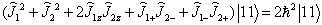                 （4）

将（3）代入（4），利用（7.3.11）及（7.3.11），得

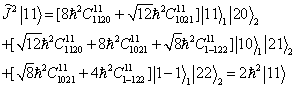                    （5）

令

              

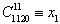
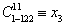
得

 

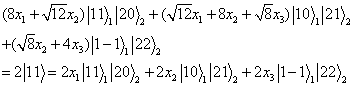
比较系数得

 

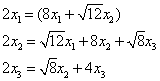
利用归一化可得

 

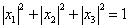
取相因子为零，经简单计算得

 

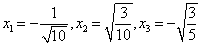
从而 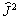和 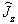的共同本征函数 为

 

例3   一个真实的He原子的基态是不退化的。我们设想一“He原子”，

其内两个电子用两个自旋为1的带相同负电、相同质量的粒子代替之。
略去与自旋相关的作用力。对于这一假想的原子，计算其基态简并度。

由于自旋为整数，且它们的各种固有属性（电荷、质量、自旋）均相同，
实验表明这样的原子的总波函数应该是对称的。由于不存在与自旋相关的力，
因此总波函数 可以写为空间部分与自旋部分的乘积。在基态时，空间部分的
波函数总是对称的，故而自旋部分的波函数也应该是对称的。自旋波函数对称
与否取决于因子

 

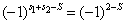
总自旋量子数的取值，按 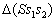应为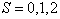

为使自旋部分波函数对称，S取为  

   由于力场与S无关，故能量相对于自旋量子数 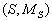退化度为

 

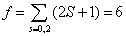
因此假想的“He原子”基态退化度为6。