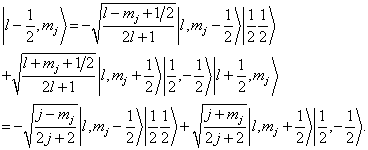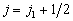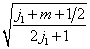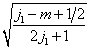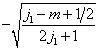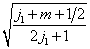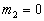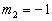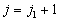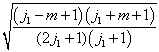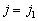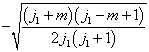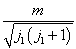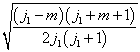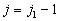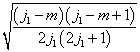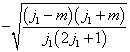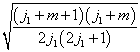由于(7.4.12), 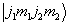 一般说来不能是
一般说来不能是
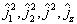 的共同本征矢。
的共同本征矢。
但由于

是完备本征函数集,
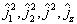 的共同本征矢集
的共同本征矢集
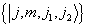 可由
可由
 叠加得到。
叠加得到。
由(7.4.15)可知,
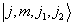 的各叠加项必满足条件
的各叠加项必满足条件
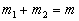 ,
,
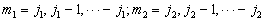 。
。
由此应有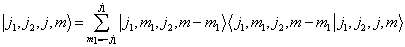
非耦合表象到耦合表象的变换是一个么正变换,是非奇变换,因此耦合表象 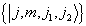 也是
也是 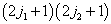 维。
维。
由角动量理论可知,
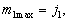
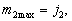 因此
因此 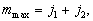 由此得
由此得  相应于
相应于  ,
, 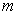 有
有  取值,
取值,
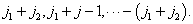
下面我们分析 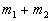 的各种可能取值。
的各种可能取值。

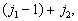

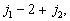

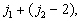
.....
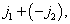

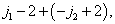 ……
……

.....
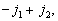
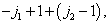
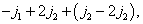 ……
……

......

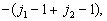
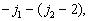


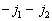
由上式可看到,第一列有 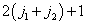 个
个  的可能取值,且相差为1,相应于角动量量子数
的可能取值,且相差为1,相应于角动量量子数 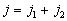 ,第二列有
,第二列有 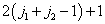 个
个 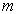 的可能取值,且相差为1,相应于角动量量子数
的可能取值,且相差为1,相应于角动量量子数 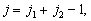 第三列有
第三列有  个
个 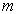 的可能取值,且相差为1,相应于角动量量子数
的可能取值,且相差为1,相应于角动量量子数  ……第
……第 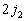 列有
列有 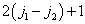 个
个 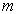 的可能取值,且相差为1,相应于角动量量子数
的可能取值,且相差为1,相应于角动量量子数 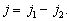 上式同行之间
上式同行之间 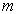 相同,但不同的列相应的
相同,但不同的列相应的 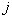 不同;同列之间
不同;同列之间 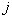 相同,但不同的行相应的
相同,但不同的行相应的 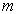 不同。因此上式每一项都代表
不同。因此上式每一项都代表 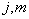 不同的态。共有
不同的态。共有
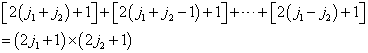
个 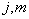 不同的态。这与无耦合表象态空间的维数相同,因此这些构成了耦合表象的一个完全集。量子数
不同的态。这与无耦合表象态空间的维数相同,因此这些构成了耦合表象的一个完全集。量子数 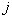 取值
取值
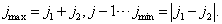
将耦合表象的基用无耦合表象的基展开时的展开系数,即
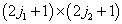 维子空间中耦合表象的基矢与无耦合表象的基矢之间么正变换的矩阵元
维子空间中耦合表象的基矢与无耦合表象的基矢之间么正变换的矩阵元 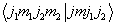 称为Clebsch-Gordan系数。显然,仅当
称为Clebsch-Gordan系数。显然,仅当 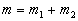 及
及 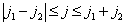 时,
时,  才不为零。表象的基矢有位相不定性,因而么正变换的矩阵元
才不为零。表象的基矢有位相不定性,因而么正变换的矩阵元  也有位相不定性。适当取位相可使
也有位相不定性。适当取位相可使  为实。这里不讨论Clebsch-Gordan系数的性质及计算,仅作为例子给出如下两个表。
为实。这里不讨论Clebsch-Gordan系数的性质及计算,仅作为例子给出如下两个表。
表1
|
|
|
|
|
|
|
|
|
|
|
|
表2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
作为例子,可由表1求得两个 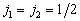 的两个角动量相加后的可能态。
的两个角动量相加后的可能态。
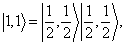 (7.4.16)
(7.4.16)
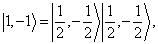 (7.4.17)
(7.4.17)
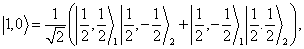 (7.4.18)
(7.4.18)
 (7.4.19)
(7.4.19)
前三个是  的三重态,
的三重态, 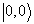 是独态。
是独态。
由表1求得两个 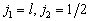 的两个角动量相加后的可能态。
的两个角动量相加后的可能态。
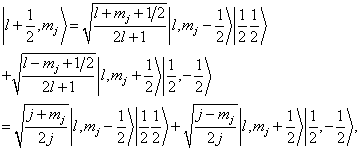 (7.4.20)
(7.4.20)