§4
角动量加法的一般问题
角动量算符的定义及性质
(1)一般地说,若一向量算符  的分量满足
的分量满足
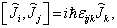
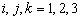 ,
(7.4.1)
,
(7.4.1)
则称
 是角动量算符。
是角动量算符。
(2)角动量算符的平方
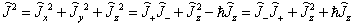 , (7.4.2)
, (7.4.2)
其中
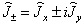
(3)  和
和
 的每个分量均对易,例如,
的每个分量均对易,例如,
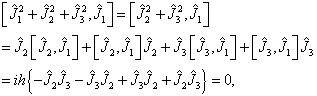 (7.4.3)
(7.4.3)
同理, 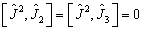 。
。
(4)令 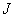 是
是  的量子数,
的量子数, 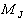 是
是  的量子数,则
的量子数,则  和
和  的共同完备本征函数系为
的共同完备本征函数系为
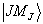
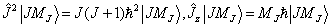 (7.4.5)
(7.4.5)
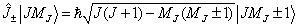 (7.4.6)
(7.4.6)
二、角动量加法
(1)总角动量算符
若 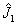 和
和 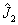 是两个无关的角动量算符,即
是两个无关的角动量算符,即
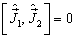 ,
(7.4.7)
,
(7.4.7)
则这两个角动量算符可以相加,
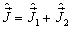 。
(7.4.8)
。
(7.4.8)
利用(7.4.7)容易证明, 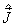 仍然满足(7.4.1), 因此
仍然满足(7.4.1), 因此  仍然是角动量算符,称为总角动量。总角动量的平方
仍然是角动量算符,称为总角动量。总角动量的平方
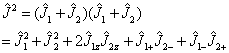 (7.4.9)
(7.4.9)
在此,利用了
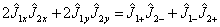
总角动量算符的升降算符为
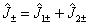
(2)至此我们已有了以下角动量算符:
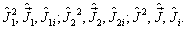 ,
,
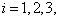
它们之间的对易关系有:
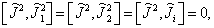 (7.4.10)
(7.4.10)
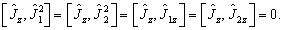 (7.4.11)
(7.4.11)
应该特别注意到
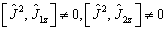 。
(7.4.12)
。
(7.4.12)
(3)总角动量的本征值谱
非耦合表象
由于 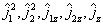 (由于(7.4.8),其中只有4个是独立的)相互对易,所以它们有共同完备本征函数系
(由于(7.4.8),其中只有4个是独立的)相互对易,所以它们有共同完备本征函数系 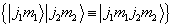 ,即,
,即,
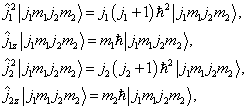 (7.4.14)
(7.4.14)
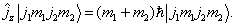 (7.4.15)
(7.4.15)
这些基矢 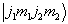 是由
是由 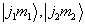 相乘得到,所以称为非耦合表象,且显然是
相乘得到,所以称为非耦合表象,且显然是 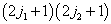 维。
维。
耦合表象
由于 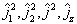 也是相互对易的,所以它们也有共同完备本征函数系,称为耦合表象。
也是相互对易的,所以它们也有共同完备本征函数系,称为耦合表象。