习题选讲7
例题7.1
设 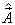 和
和 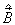 是与
是与  对易的两个矢量算符,证明
对易的两个矢量算符,证明
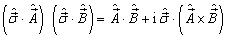
证明:将等式左端写成三个矢量的分量形式,即
 (1)
(1)
利用
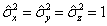 (2)
(2)
及
 (3)
(3)
得到
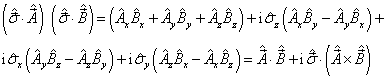 (4)
(4)
例题7.2
求自旋算符在 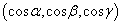 方向投影
方向投影

的本征值和相应的本征矢。在其两个本征态上,求  的取值几率和平均值。
的取值几率和平均值。
解:将三个自旋分量算符代入自旋算符的投影 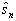 中,得到其矩阵表示为
中,得到其矩阵表示为
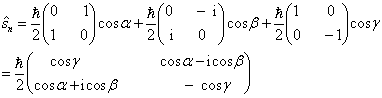 (1)
(1)
设
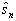 的本征值为
的本征值为 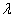 ,则其满足的本征方程为
,则其满足的本征方程为
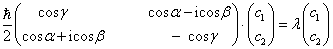 (2)
(2)
相应的久期方程为
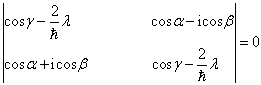 (3)
(3)
解之得
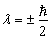 (4)
(4)
上式表明,自旋在任意方向的投影的本征值总是 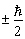 。
。
为了求出 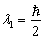 相应的本征矢,将其代入(2)式,得到
相应的本征矢,将其代入(2)式,得到
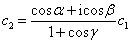 (5)
(5)
再利用归一化条件
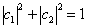 (6)
(6)
得到归一化的本征矢为
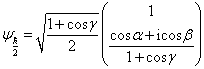 (7)
(7)
同理可以求出 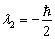 相应的本征矢为
相应的本征矢为
 (8)
(8)
在本征态 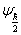 上,
上, 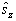 的取值几率为
的取值几率为
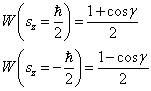 (9)
(9)
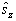 的平均值为
的平均值为
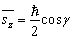 (10)
(10)
同理可以求出,在本征态 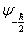 上,
上,
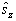 的取值几率为
的取值几率为
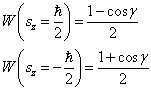 (11)
(11)
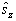 的平均值为
的平均值为
 (12)
(12)