例题7.3
自旋为 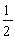 的粒子处于线谐振子位势中,若
的粒子处于线谐振子位势中,若  时,粒子的状态为
时,粒子的状态为
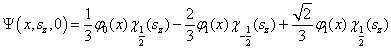
其中, 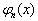 是线谐振子的第
是线谐振子的第  个本征态。求
个本征态。求 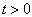 时粒子的波函数、能量的取值几率与平均值。
时粒子的波函数、能量的取值几率与平均值。
解:求解粒子满足的定态薛定谔方程
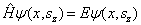 (1)
(1)
因为哈密顿算符与自旋变量 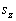 无关,所以,可以将
无关,所以,可以将  分离变量,即
分离变量,即
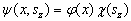 (2)
(2)
其中,写成函数形式的自旋波函数为
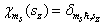 (3)
(3)
而  是线谐振子的解。于是,得到
是线谐振子的解。于是,得到
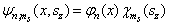 (4)
(4)
应该注意到,在计及自旋且哈密顿算符不含自旋变量时,粒子的能量对自旋磁量子数是二度简并的。
将 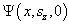 归一化。
归一化。
 (5)
(5)
于是,有
 (6)
(6)
或者,直接由
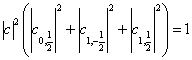 (7)
(7)
得到(6)式。归一化后的波函数为
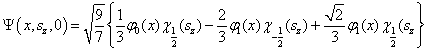
求出 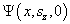 向
向 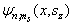 展开的展开系数。
展开的展开系数。
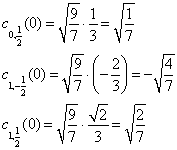 (9)
(9)
写出
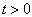 时的波函数
时的波函数
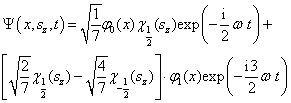 (10)
(10)
求能量的取值几率与平均值。
首先,在
 的状态中,
的状态中,
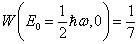 ;
;
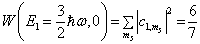 (11)
(11)
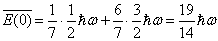 (12)
(12)
其次,在
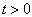 的状态中,由于,
的状态中,由于,
 (13)
(13)
所以,哈密顿量为守恒量,它的取值几率与平均值不随时间改变,与
 时的结果是一样的。
时的结果是一样的。
以上求解过程是在自旋波函数为函数形式下进行的,当然,也可以在矩阵形式下求解此问题。自旋波函数的矩阵形式为
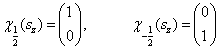 (14)
(14)
 (15)
(15)
能量的平均值为
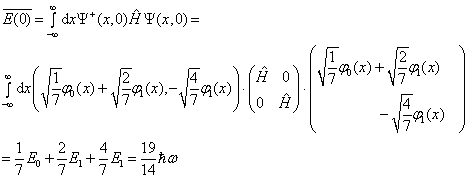 (16)
(16)