例题7.4
固有磁矩为  的质子,
的质子,  时处于
时处于 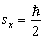 的状态,同时进入均匀磁场
的状态,同时进入均匀磁场 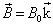 中。求
中。求 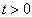 时测量
时测量 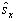 得
得 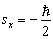 的几率是多少。
的几率是多少。
解:按如下步骤求解:
第一步,解定态薛定谔方程。
这是一个讨论自旋状态随时间演变的问题,故可以不顾及空间自由度。磁矩与外磁场相互作用引起一附加能量,与自旋相关的哈密顿算符为
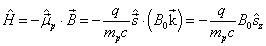 (1)
(1)
其中, 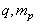 分别为质子的电荷与质量。若令
分别为质子的电荷与质量。若令
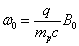 (2)
(2)
则哈密顿算符可简化为
 (3)
(3)
在 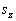 表象中,哈密顿算符是对角矩阵,已知它的解为
表象中,哈密顿算符是对角矩阵,已知它的解为
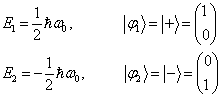 (4)
(4)
第二步,写出任意时刻的波函数。
依题意,知
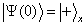 (5)
(5)
式中, 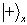 是在
是在 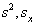 表象中
表象中 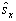 的一个本征矢,为了将其在
的一个本征矢,为了将其在
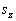 表象中表示出来,必须求解
表象中表示出来,必须求解
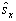 满足的本征方程,即
满足的本征方程,即
 (6)
(6)
解之得
 (7)
(7)
在
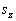 表象中,初态为
表象中,初态为
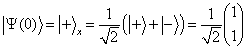 (8)
(8)
于是,
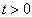 时刻的波函数为
时刻的波函数为
 (9)
(9)
第三步,求在
![]() 态上测量
态上测量
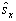 得
得 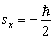 的几率。
的几率。
将
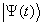 向
向
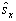 的本征态展开
的本征态展开
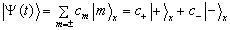 (10)
(10)
其中,
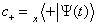 ;
;
 (11)
(11)
在
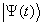 态上测量
态上测量
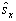 得
得 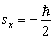 的几率为
的几率为
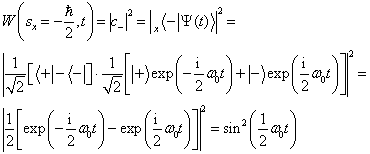 (12)
(12)
第四步,对上述结果进行讨论。
在 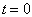 时,质子处于
时,质子处于 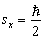 的状态上,在均匀磁场的作用下,使其在
的状态上,在均匀磁场的作用下,使其在
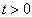 时刻以
时刻以 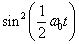 的几率处于
的状态。
的几率处于
的状态。
令
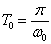 (13)
(13)
则
 (14)
(14)
当 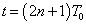 时,
时,
 (15)
(15)
当 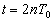 时,
时,
 (16)
(16)
总之,质子进入均匀磁场后,随着时间的推移,其状态在 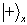 与
与 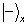 之间作周期性的“翻转”。
之间作周期性的“翻转”。