§7.
3 升降算符
升降算符在角动量计算中起着重要的作用,尽管它本身并不直接描述任何可观测量。
一.定义
 ,
(7.3.1)
,
(7.3.1)
其中 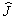 为任意角动量算符,
为任意角动量算符, 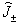 分别称为升,降算符。由(3。1)式可得
分别称为升,降算符。由(3。1)式可得
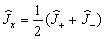 ,
, 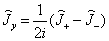 。
(7.3.2)
。
(7.3.2)
二.性质、对易关系及有关公式
容易由定义得到:
 (7.3.3)
(7.3.3)
 (7.3.4)
(7.3.4)
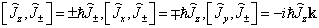 (7.3.5)
(7.3.5)
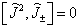 (7.3.6)
(7.3.6)
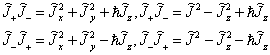 (7.3.7)
(7.3.7)
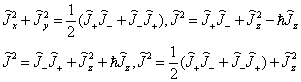 (7.3.8)
(7.3.8)
三.
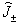 的作用
的作用
用 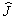 表示任意角动量,用j表示
表示任意角动量,用j表示 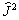 的量子数,用
的量子数,用 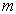 表示
表示 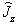 的量子数,则
的量子数,则 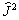 ,
, 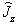 共同本征函数可表示为
。下面证明
共同本征函数可表示为
。下面证明
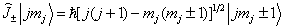 (7.3.9)
(7.3.9)
可见,将算符 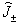 作用到
作用到 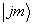 上后,将会得到一个新得本征态矢
上后,将会得到一个新得本征态矢 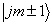 ,此态矢的量子数
,此态矢的量子数 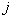 不变,但磁量子数
不变,但磁量子数 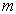 将分别递增和递减1,变为
将分别递增和递减1,变为 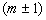 。这也是
。这也是 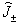 称为升.降算符的原因。这一公式在应用上相当重要。为了证明该式,让我们分两步讨论。
称为升.降算符的原因。这一公式在应用上相当重要。为了证明该式,让我们分两步讨论。
第一步:证明公式  成立。其中
成立。其中 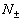 为归一化因子。
为归一化因子。
以 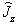 作用在
作用在  上,并利用(7.3.5)式的第一式,得
上,并利用(7.3.5)式的第一式,得
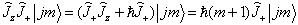 (7.3.10)
(7.3.10)
由上式可以看出  仍然是
仍然是 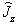 的本征函数,但对应的磁量子数已不再是
的本征函数,但对应的磁量子数已不再是 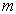 ,而是
,而是 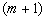 了。因此
了。因此  与
与 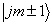 至多相差一常数因子,即
至多相差一常数因子,即
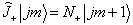 (7.3.11)
(7.3.11)
类似地,有
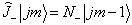 (7.3.12)
(7.3.12)
第二步:求归一化因子  。由
。由
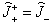 ,(7.3.11)及(7.3.7)式得
,(7.3.11)及(7.3.7)式得
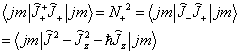 (7.3.13)
(7.3.13)
由
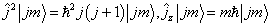
及归一化条件,即得
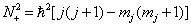 ,
,
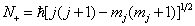 (7.3.14)
(7.3.14)
类似地可得
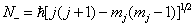 (7.3.15)
(7.3.15)
 为实数。从而(7.3.9)式得证。
为实数。从而(7.3.9)式得证。