§8.5
跃迁
§8.5.1 含时微扰
哈密顿算符与时间有关时,
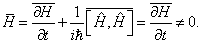
能量不再是守恒量,因而薛定谔方程
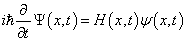 (8.5.1)
(8.5.1)
这时不存在定态解。含时哈密顿将导致体系状态发生变化,即,由一种状态跃迁到另一种状态。这时的核心问题是求出跃迁振幅。由于(8.5.1)是时间的一阶微分方程,只要给定初始状态,就能确定任意时刻体系的状态。准确求解(8.5.1)就能得到跃迁振幅。但是,一般情况下,很难准确求解(8.5.1),为此,更实际的是找到求解(8.5.1)的近似方法。以下三种情况较容易求得近似解:
1.
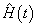 可以写为
可以写为
 (8.5.2)
(8.5.2)
且
 (8.5.3)
(8.5.3)
式中,
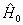 与时间无关,
与时间无关,
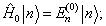 (8.5.4)
(8.5.4)
2.
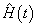 在很短的时间内从一种形式突变到另一种形式,而在其它时间
在很短的时间内从一种形式突变到另一种形式,而在其它时间 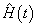 与
与
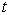 无关,这时可以用“突变近似法”讨论;
无关,这时可以用“突变近似法”讨论;
3.
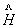 随
随
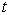 的变化非常缓慢,这时可以用“浸渐近似法”讨论。
的变化非常缓慢,这时可以用“浸渐近似法”讨论。
本节我们仅讨论第一种情况。
A.在
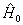 表象中求解含时薛定谔方程
表象中求解含时薛定谔方程
由于
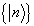 是完备集,(8.5.1)的、初始
是完备集,(8.5.1)的、初始
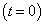 处于
处于
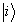 态的解
态的解
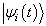 能向
能向
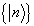 展开。
展开。
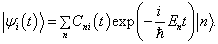 (8.5.5)
(8.5.5)
代入(8.5.1)式,且以
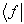 作用于两边,得
作用于两边,得
 (8.5.6)
(8.5.6)
其中
 (8.5.7)
(8.5.7)
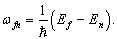 (8.5.8)
(8.5.8)
(8.5.6)是在
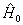 表象中的与时间相关的薛定谔方程。
表象中的与时间相关的薛定谔方程。