B.
一级近似解
把微扰项
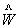 作为一级小量,一级近似解为
作为一级小量,一级近似解为
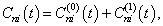 (8.5.9)
(8.5.9)
这里将
 也看作一级小量,将其代入(8.5.6),精确到一级小量
也看作一级小量,将其代入(8.5.6),精确到一级小量
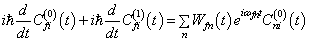
并比较同量级的系数,分别得“零级”及“一级”系数方程
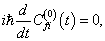 (8.5.10)
(8.5.10)
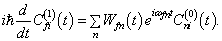 (8.5.11)
(8.5.11)
(8.5.10)的解是一个与时间无关的数
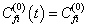 (8.5.12)
(8.5.12)
因为
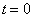 时,体系处于
时,体系处于 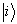 态,所以
态,所以
 (8.5.13)
(8.5.13)
(8.5.11)式的解是
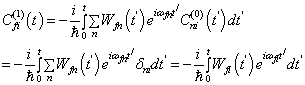 (8.5.14)
(8.5.14)
(8.5.14)即为一级近似波函数修正值。由(8.5.14)可得由初态 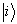 跃迁到末态
跃迁到末态
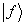 的概率是
的概率是
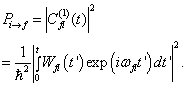 (8.5.15)
(8.5.15)
由(8.5.15)可知,由(8.5.5)成立的条件是(8.5.3),否则就不可以用
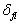 代替
代替
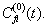 当前实验上一般对与跃迁相关联的光谱线的强度(或相应的激发态的寿命)的观测数据只有两三位有效数字。这样如果一级微扰非零,一般就不必再计算高级微扰了。由(8.5.5)可知,处于初态
当前实验上一般对与跃迁相关联的光谱线的强度(或相应的激发态的寿命)的观测数据只有两三位有效数字。这样如果一级微扰非零,一般就不必再计算高级微扰了。由(8.5.5)可知,处于初态 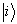 的体系,由于
的体系,由于
 的作用,
的作用,
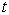 时刻是若干态的叠加。在这一叠加态中,体系处于
时刻是若干态的叠加。在这一叠加态中,体系处于
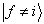 态的概率是
态的概率是
 。
。
由(8.5.15)可知,跃迁概率决定于与初末态及  的性质。如果由于
的性质。如果由于  的对称性,
的对称性,
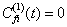 ,则
,则
 ,即
,即 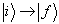 的跃迁被禁戒。这样就可由
的跃迁被禁戒。这样就可由  的对称性而得到选择定则。
的对称性而得到选择定则。
由(8.5.15)及
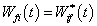 可看出,
可看出,
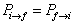 ,这个结果对于
,这个结果对于
 态与
态与
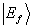 态都无简并或
态都无简并或
 态与
态与
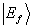 态简并度相同时是正确的。对于测量说来,当
态简并度相同时是正确的。对于测量说来,当
 态与
态与
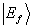 态有简并时,一般不能区分哪一个初态(体系等概率的处于各简并态)跃迁到哪一个末态,因此计算跃迁概率时应对每一个初态跃迁到所有末态的概率求和后求平均。例如,中心力场单粒子能级
态有简并时,一般不能区分哪一个初态(体系等概率的处于各简并态)跃迁到哪一个末态,因此计算跃迁概率时应对每一个初态跃迁到所有末态的概率求和后求平均。例如,中心力场单粒子能级
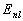 简并度是
简并度是
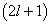 ,这样
,这样
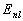 能级跃迁到
能级跃迁到 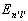 能级时的跃迁概率就是
能级时的跃迁概率就是
 (8.5.16)
(8.5.16)
由(8.5.16)可见,当初末态简并度不同时,跃迁概率就不再相同。
一个经典体系由一个能量为
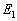 的状态过渡到另一个能量为
的状态过渡到另一个能量为
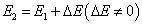 的状态时,所用时间必是有限的。与此不同,一个量子体系由
的状态时,所用时间必是有限的。与此不同,一个量子体系由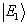 状态跃迁到
状态跃迁到
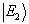 状态时,所用时间是零,即量子跃迁是瞬时发生的。
状态时,所用时间是零,即量子跃迁是瞬时发生的。