§8.5.2
几种常见的含时微扰
1.
周期性微扰
设
 在
在
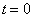 加入,在
加入,在
 撤出,且
撤出,且
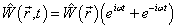 ,
(8.5.17)
,
(8.5.17)
则称
 为周期性微扰或简谐微扰。
为周期性微扰或简谐微扰。
根据§8.5中的(8.5.14)式,简谐微扰时的一级近似修正值为
 (8.5.18)
(8.5.18)
式中
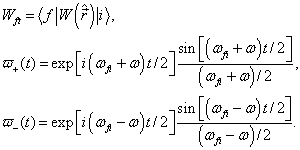 (8.5.19)
(8.5.19)
由(8.5.18)不难看出,当分母趋于零时,
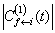 有显著大的值。
有显著大的值。
1.当  时
时
由于  ,因此这种情况相当于
,因此这种情况相当于
 的情况。略去(8.5.18)第一项,有
的情况。略去(8.5.18)第一项,有
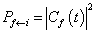
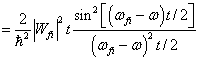 (8.5.20)
(8.5.20)
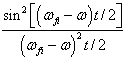 随
随
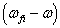 变化如图8.
2所示
变化如图8.
2所示
(令 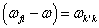 ,
, 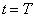 )。
)。
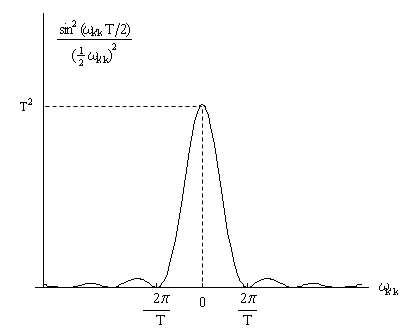
图8.
2
利用
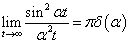
当  ,由(8.5.20)得
,由(8.5.20)得
 (8.5.21)
(8.5.21)
由(8.5.21)可以看出,跃迁过程能量守恒,
跃迁几率正比于微扰作用的时间 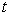 。足够长时间后,
单位时间的跃迁概率,
即跃迁速率
。足够长时间后,
单位时间的跃迁概率,
即跃迁速率
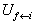 与时间无关,
与时间无关,
 (8.5.22)
(8.5.22)
由(8.5.22)可以看出,当
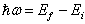 (8.5.23)
(8.5.23)
时,才能跃迁。
2. 当 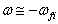 时
时
这种情况相当于 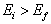 的情况。略去(8.5.18)第二项,同理可得
的情况。略去(8.5.18)第二项,同理可得
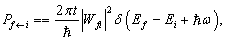 (8.5.24)
(8.5.24)
 (8.5.25)
(8.5.25)
2.常微扰
在(
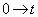 )的时间间隔内,量子体系受到一个与时间无的微扰作用
)的时间间隔内,量子体系受到一个与时间无的微扰作用
 (8.5.26)
(8.5.26)
实际上,常微扰是ω=0时的简谐微扰。
以吸收辐射为例讨论这种微扰。由(8.5.25)得
 (8.5.27)
(8.5.27)
对于初态具有确定的能量 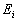 ,而末态却是能级在
,而末态却是能级在 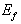 附近连续态。设末态的能级密度为
附近连续态。设末态的能级密度为 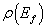 ,则在
,则在  之间的态的数目为
之间的态的数目为 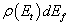 ,从而由(8.5.27)可给出总的跃迁速率为
,从而由(8.5.27)可给出总的跃迁速率为
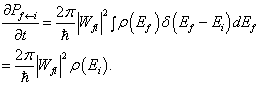 (8.5.27)
(8.5.27)
上式说明在常微扰下,只有 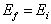 时才会发生量子跃迁。利用(8.5.27)的结果处理弹性散射是很方便的。(8.5.27)称为黄金规则(Golden
rule).
时才会发生量子跃迁。利用(8.5.27)的结果处理弹性散射是很方便的。(8.5.27)称为黄金规则(Golden
rule).