§8.2.
简并态能量的一级微扰修正
当
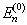简并或
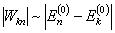，以上微扰方法就不再适用，需推导出新的微扰方法。本节给出
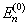简并时的一级微扰修正。设
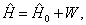且已知
（8.2.1）
求解
（8.2.2）
作为（8.2.2）的准确解，
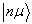应向
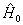的所有本征矢展开，包括所有能级的简并及非简并本征矢。求（8.2.2）的准确解是冗长、困难的工作。但其一级修正却可以由下面的分析较容易地得到。
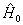的能级
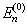之所以有简并，是由于
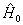具有某种对称性。 
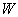加入后则破坏了这种对称性，因此 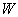能部分或全部消除简并。
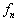个本征矢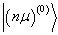 
或它们的任意组合对于
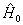是对称的，但对于 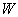就可能不再是对称的。因此将
个 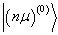适当组合后就可能部分或全部消除简并。根据这种思路，我们首先给出
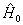能级
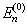的本征矢一般形式，
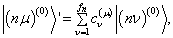（8.2.3）
并将（8.2.2）中的
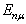写为
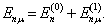（8.2.4）
将（8.2.3）及（8.2.4）代入（8.2.2），得
（8.2.5）
将（8.2.5）左乘
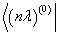，考虑到
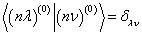
及
，
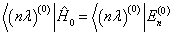得
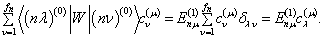（8.2.6）
写为矩阵形式，有
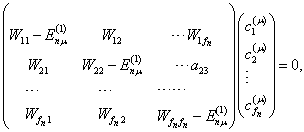（8.2.7）
式中
。
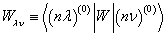（8.2.7）有非零解的条件是其系数行列式为零，即
（8.2.8）
这是一个以
为未知数的
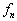次方程。解此方程，最多可得
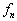个不同的实根，这时就完全消除了简并。将所得的根代入（8.2.7），求解
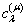，并利用归一化条件，由（8.2.3）就得到了与能量本征值
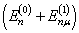相应的零级波矢量。进一步，如果能级差还满足（8.1.17），则可用非微扰公式求得高级修正。如果不同根的数目小于
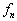，则仅仅部分消除了简并，还需用各种近似方法进一步计算。能够证明，这样得到的、相应于不同
的零级波矢量是正交的，仍然简并能级的零级波矢量也能使它们彼此正交。当然，每一个零级波矢量也都能是归一的。