§8
阅读材料(苏汝铿,量子力学,
第250页,复旦大学出版社
1990)
1.重新组合后的零级波函数相互正交的证明
经过重新组合后的零级波函数 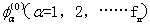 相互正交,满足
相互正交,满足
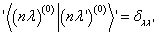 (8.2.9)
(8.2.9)
现在来证明(8.2.9)式。将由久期方程解出的根代入(8.2.7)后,有
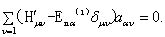 (8.2.10)
(8.2.10)
它的复共轭式是
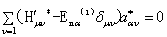 .
(8.2.11)
.
(8.2.11)
为计算方便起见,将(8.2.11)的脚标 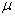 与
与  互换,并记
互换,并记 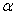 为
为 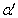 ,得
,得
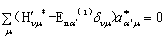 .
(8.2.12)
.
(8.2.12)
以 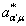 乘(8.2.10),并对
乘(8.2.10),并对
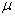 求和;以
求和;以 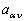 乘(8.2.12)式,并对
乘(8.2.12)式,并对
 求和,再将所得的两式相减,注意到
求和,再将所得的两式相减,注意到 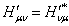 ,得
,得
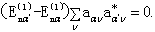 (8.2.13)
(8.2.13)
可见,若简并完全消除,无重根时, 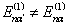 ,必有
,必有 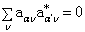 。若仍存在简并,虽则对于与
。若仍存在简并,虽则对于与 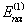 重根对应的波函数,我们并不能由(8.2.13)直接证明它们正交,但总可利用对简并波函数正交性相同的讨论,选取适当的组合使这些简并的波函数正交化。综合上述,在适当选择归一常数后总能得出
重根对应的波函数,我们并不能由(8.2.13)直接证明它们正交,但总可利用对简并波函数正交性相同的讨论,选取适当的组合使这些简并的波函数正交化。综合上述,在适当选择归一常数后总能得出 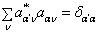 ,即重新组合后的零级波函数
,即重新组合后的零级波函数 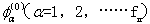 彼此相互正交.
彼此相互正交.
用微扰论求解时,若能利用对称性选择零级波函数以尽量使 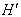 对角化,可以使讨论和计算简化。
对角化,可以使讨论和计算简化。