§8.3
氢原子的斯塔克效应
在外电场中,原子光谱会发生劈裂,称之为斯塔克(Stark)效应。作为微扰论的一个应用实例,下面讨论氢原子的一级斯塔克效应。
以氢原子为例,暂不顾及电子的自旋,电子受到一个库仑场的作用,能级由主量子数
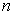 决定,简并度为
决定,简并度为 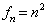 。若外加一个沿
。若外加一个沿 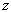 方向的电场,则位势的对称性部分地被破坏,能级将产生劈裂,简并就会部分地被消除。
方向的电场,则位势的对称性部分地被破坏,能级将产生劈裂,简并就会部分地被消除。
在上述外电场中,氢原子的哈密顿算符为
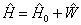 (8.3.1)
(8.3.1)
式中,
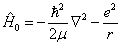 (8.3.2)
(8.3.2)
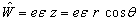 (8.3.3)
(8.3.3)
当电场强度 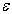 较小时,
较小时, 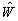 可以看作微扰。
可以看作微扰。
无微扰时,已知氢原子哈密顿算符 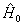 的本征解为
的本征解为
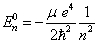 (8.3.4)
(8.3.4)
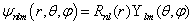 (8.3.5)
(8.3.5)
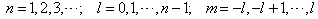
基态能级一级修正
当氢原子处于基态时,其量子数
 ,
,  ,
,
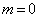 ,此时,简并度
,此时,简并度
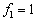 ,即无简并存在。应用无简并微扰论,能量的一级修正为
,即无简并存在。应用无简并微扰论,能量的一级修正为
 (8.3.6)
(8.3.6)
式中利用了
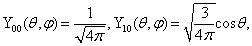 (8.3.7)
(8.3.7)
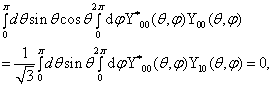 (8.3.8)
(8.3.8)
可见,氢原子的基态在电场中并不产生劈裂。
第一激发态能级的一级修正
当氢原子处于第一激发态时,其量子数 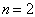 ,
,
 ,当
,当
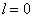 时,只有
时,只有
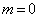 ;当
;当 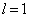 时,
时, 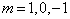 。氢原子的第一激发态是四度简并的,四个零级波函数分别简记为
。氢原子的第一激发态是四度简并的,四个零级波函数分别简记为
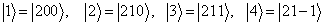 (8.3.9)
(8.3.9)
在此基底之下,计算微扰矩阵元
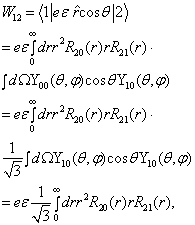 (8.3.10)
(8.3.10)
考虑到
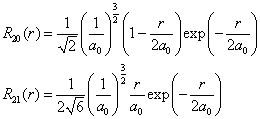 (8.3.11)
(8.3.11)
其中,
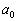 为玻尔半径,得到矩阵元的径向部分为
为玻尔半径,得到矩阵元的径向部分为
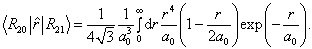 (8.3.12)
(8.3.12)
令
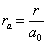 (8.3.13)
(8.3.13)